题目内容
8.小李参加一种红包接龙游戏:他在红包里塞了12元,然后发给朋友A,如果A猜中,A将获得红包里的所有金额;如果A未猜中,A将当前的红包转发给朋友B,如果B猜中,A、B平分红包里的金额;如果B未猜中,B将当前的红包转发给朋友C,如果C猜中,A、B和C平分红包里的金额;如果C未猜中,红包里的钱将退回小李的账户,设A、B、C猜中的概率分别为$\frac{1}{3}$,$\frac{1}{2}$,$\frac{1}{3}$,且A、B、C是否猜中互不影响.(Ⅰ)求A恰好获得4元的概率;
(Ⅱ)设A获得的金额为X元,求X的分布列及X的数学期望.
分析 (1)根据相互独立事件的概率公式计算即可;
(2)由题意,X的可能取值为0,4,6,12,计算对应的概率值,写出X的分布列与数学期望值.
解答 解:(1)A恰好获得4元的概率为$\frac{2}{3}$×$\frac{1}{2}$×$\frac{1}{3}$=$\frac{1}{9}$;…(2分)
(2)X的可能取值为0,4,6,12,
则P(X=4)=$\frac{1}{9}$,P(X=0)=$\frac{2}{3}$×$\frac{1}{2}$×$\frac{2}{3}$=$\frac{2}{9}$,
P(X=6)=$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{3}$,P(X=12)=$\frac{1}{3}$,…(5分)
所以X的分布列为:
| X | 0 | 4 | 6 | 12 |
| P | $\frac{2}{9}$ | $\frac{1}{9}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
点评 本题考查了相互独立事件的概率计算以及离散型随机变量的分布列与数学期望问题,是基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
3.直线$\sqrt{3}x+3y+a=0$的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
13.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
20.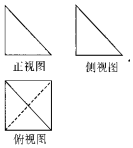 如图所示,某几何体的三视图中,正视图和俯视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )
如图所示,某几何体的三视图中,正视图和俯视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )
 如图所示,某几何体的三视图中,正视图和俯视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )
如图所示,某几何体的三视图中,正视图和俯视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | $1+\sqrt{2}$ |
17.若$\frac{1}{1+a}>1-a$,则实数a的取值范围是( )
| A. | a>0 | B. | a>1 | C. | a>-1且a≠0 | D. | a<0 |
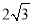 cm
cm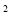 B.
B.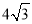 cm2
cm2