题目内容
20.已知曲线C的极坐标方程为2ρsinθ+ρcosθ=10,以极点为直角坐标系原点,极轴所在直线为x轴建立直角坐标系,曲线C1的参数方程为${C_1}:\left\{\begin{array}{l}x=3cosα\\ y=2sinα\end{array}\right.$(α为参数),.(Ⅰ)求曲线C的直角坐标方程和曲线C1的普通方程;
(Ⅱ)若点M在曲线C1上运动,试求出M到曲线C的距离的最小值及该点坐标.
分析 (1)直接由x=ρcosθ,y=ρsinθ及已知可得曲线C的直角坐标方程,把${C_1}:\left\{\begin{array}{l}x=3cosα\\ y=2sinα\end{array}\right.$变形,利用平方关系消参可得曲线C1的普通方程;
(2)设出点M的坐标,利用点到直线的距离公式及三角函数的辅助角公式化积得答案.
解答 解:(1)由2ρsinθ+ρcosθ=10,得x+2y-10=0,
∴曲线C的普通方程是:x+2y-10=0.
由$\left\{\begin{array}{l}x=3cosα\\ y=2sinα\end{array}\right.$,得$\left\{\begin{array}{l}cosα=\frac{x}{3}\\ sinα=\frac{y}{2}\end{array}\right.$,代入cos2α+sin2α=1,得$\frac{x^2}{9}+\frac{y^2}{4}=1$,
∴曲线C1的普通方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$;
(2)曲线C的普通方程是:x+2y-10=0,
设点M(3cosα,2sinα),由点到直线的距离公式得:
$d=\frac{{|{3cosα+4sinα-10}|}}{{\sqrt{5}}}=\frac{1}{{\sqrt{5}}}|{5cos(α-φ)-10}|$,其中$cosφ=\frac{3}{5},sinφ=\frac{4}{5}$,
∴α-φ=0时,${d_{min}}=\sqrt{5}$,此时$M(\frac{9}{5},\frac{8}{5})$.
点评 本题考查简单曲线的极坐标方程,考查参数方程化普通方程,训练了点到直线距离公式的应用,是中档题.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案| A. | 0.76<log0.76<60.7 | B. | log0.76<0.76<60.7 | ||
| C. | log0.76<60.7<0.76 | D. | 0.76<60.7<log0.76 |
| A. | $-\frac{1}{3}$ | B. | -3 | C. | $-\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
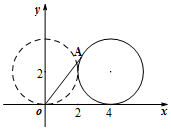 如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).
如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).