题目内容
12.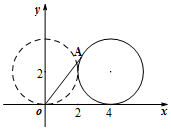 如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).
如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).
分析 设滚动后的圆的圆心为O',切点为C(4,0),连接O'A,过O'作与x轴正方向平行的射线,交圆O'于B(6,2),设∠BO'A=θ,则根据圆的参数方程,得P的坐标,再根据圆的圆心从(0,2)滚动到(4,2),算出θ,结合三角函数的诱导公式,化简可得A的坐标.
解答 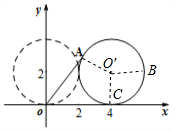 解:设滚动后的圆的圆心为O',切点为C(4,0),连接O'A,
解:设滚动后的圆的圆心为O',切点为C(4,0),连接O'A,
过O'作与x轴正方向平行的射线,交圆O'于B(6,2),设∠BO'A=θ,
∵⊙O'的方程为(x-4)2+(y-2)2=4,
∴根据圆的参数方程,得A的坐标为(4+2cosθ,2+2sinθ),
∵单位圆的圆心的初始位置在(0,2),圆滚动到圆心位于(4,2)
∴可得θ=$\frac{3π}{2}$-2
可得cosθ=cos($\frac{3π}{2}$-2)=-sin2,sinθ=sin($\frac{3π}{2}$-2)=-cos2,
代入上面所得的式子,得到A的坐标为(4-2sin2,2-2cos2).
故答案为(4-2sin2,2-2cos2)
点评 本题根据半径为2的圆的滚动,求一个向量的坐标,着重考查了圆的参数方程和平面向量的坐标表示的应用等知识点,属于中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
2.设全集U=R,集合$A=\{x\left|{y=\sqrt{x}}\right.\},B=\{y\left|{y={{log}_2}(x-\frac{1}{2}),x∈[1,\frac{9}{2}]}\right.\}$,则(∁UA)∩B=( )
| A. | ∅ | B. | [-1,0) | C. | $[1,\frac{9}{2}]$ | D. | [0,2] |
7.函数$f(x)=\left\{\begin{array}{l}0,(x>0)\\ π,(x=0)\\ 1,(x<0)\end{array}\right.$,则f(f(f(π)))=( )
| A. | 1 | B. | 0 | C. | π | D. | π+1 |
4.已知椭圆具有性质:若M、N是椭圆上关于原点对称的两个点,点P是椭圆上的任意一点,当直线PM、PN的斜率都存在,并记为kPM,kPN时,那么kPM与kPN之积是与P点无关的定值.现将椭圆改为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),且kPM<0、kPN<0,则kPM+kPN的最大值为( )
| A. | $-\frac{2b}{a}$ | B. | $-\frac{2a}{b}$ | C. | $-\frac{{\sqrt{2}b}}{a}$ | D. | $-\frac{{\sqrt{2}b}}{a}$ |
2.函数$f(x)=lgx-\frac{11}{x}$的零点所在区间为( )
| A. | (8,9) | B. | (9,10) | C. | (10,11) | D. | (11,12) |