题目内容
1.已知正方形ABCD,E、F分别是CD、AD的中点.BE、CF交于点P.求证:(1)BE⊥CF;(2)AP=AB.分析 (1)连接BF,由已知推导出△BCE≌△CDF,从而∠PCE+∠CEP=90°,由此能证明BE⊥CF.
(2)先推导出点A、B、P、F四点共圆,从而∠AFB=∠APB,再由△ABF≌△BCE,推导出∠APB=∠ABP,由此能证明AP=AB.
解答 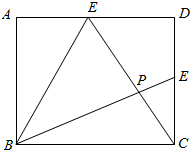 证明:(1)连接BF,
证明:(1)连接BF,
∵E、F分别是正方形ABCD的边CD和AD的中点,
∴BC=CD,∠BCE=∠CDF,CE=DF,
∴△BCE≌△CDF,
∴∠CBE=∠FCD,∠BEC=∠CFD,
∴∠PCE+∠CEP=∠DCE+∠CFD=90°,
∴BE⊥CF.
(2)∵BE⊥CF,∴∠FPB=90°,又∠DAB=90°,
∴点A、B、P、F四点共圆,∴∠AFB=∠APB,
∵AB=BC,∠ABF=∠BCE,AF=CE,
∴△ABF≌△BCE,
∴90°-∠CBE=90°-∠ABF,即∠ABP=∠AFB,
∴∠APB=∠ABP,∴AP=AB.
点评 本题考查两直线垂直和两线段相等的证明,是中档题,解题时要认真审题,注意四点共圆和三角形全等的性质的合理运用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11.己知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点为F1,F2,点A在其右半支上,若$\overrightarrow{A{F}_{1}}$•$\overrightarrow{A{F}_{2}}$=0,若∠AF1F2∈(0,$\frac{π}{12}$),则该双曲线的离心率e的取值范围为( )
| A. | (1,$\sqrt{2}$) | B. | (1,$\sqrt{3}$) | C. | ($\sqrt{2}$,$\sqrt{3}$) | D. | ($\sqrt{2}$,$\sqrt{6}$) |
12.已知a∈R且a≠0,下列各式中正确的是( )
| A. | a+$\frac{1}{a}$≥2 | B. | a+$\frac{1}{a}$≤-2 | C. | a+$\frac{1}{a}$=2 | D. | a+$\frac{1}{a}$≤-2或a+$\frac{1}{a}$≥2 |
9.若命题“若p,则q”为真命题,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知P(-1,3)为α角终边上一点,则sin(-π-α)=( )
| A. | -$\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3\sqrt{10}}{10}$ |