题目内容
13.在△ABC中,∠A=90°,AB=3,AC=2,$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=6.分析 由向量垂直的条件:数量积为0,由向量共线的知识可得$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AC}$+$\frac{2}{3}$$\overrightarrow{AB}$,再由向量的数量积的性质即可得到所求值.
解答 解:∠A=90°,AB=3,AC=2,
可得$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,
$\overrightarrow{CD}$=2$\overrightarrow{DB}$,即为$\overrightarrow{AD}$-$\overrightarrow{AC}$=2($\overrightarrow{AB}$-$\overrightarrow{AD}$),
即有$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AC}$+$\frac{2}{3}$$\overrightarrow{AB}$,
则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\overrightarrow{AB}$•($\frac{1}{3}$$\overrightarrow{AC}$+$\frac{2}{3}$$\overrightarrow{AB}$)=$\frac{1}{3}$$\overrightarrow{AB}$•$\overrightarrow{AC}$+$\frac{2}{3}$$\overrightarrow{AB}$2
=0+$\frac{2}{3}$×9=6.
故答案为:6.
点评 本题考查向量垂直的条件和向量的平方即为模的平方,考查向量共线的表示,考查运算能力,属于中档题.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
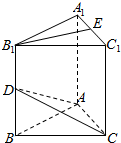 如图在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1,∠BAC=90°,点D,E分别为棱BB1,A1C1的中点,求异面直线B1E、CD所成角的余弦值.
如图在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1,∠BAC=90°,点D,E分别为棱BB1,A1C1的中点,求异面直线B1E、CD所成角的余弦值.