题目内容
11.己知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点为F1,F2,点A在其右半支上,若$\overrightarrow{A{F}_{1}}$•$\overrightarrow{A{F}_{2}}$=0,若∠AF1F2∈(0,$\frac{π}{12}$),则该双曲线的离心率e的取值范围为( )| A. | (1,$\sqrt{2}$) | B. | (1,$\sqrt{3}$) | C. | ($\sqrt{2}$,$\sqrt{3}$) | D. | ($\sqrt{2}$,$\sqrt{6}$) |
分析 设∠AF1F2=θ,由题意,|AF2|=2csinθ,|AF1|=2ccosθ,点A在其右半支上,可得2ccosθ-2csinθ=2a,求出离心率,再利用三角函数知识,即可求解.
解答 解:设∠AF1F2=θ,则
由题意,|AF2|=2csinθ,|AF1|=2ccosθ,
∵点A在其右半支上,
∴2ccosθ-2csinθ=2a,
∴e=$\frac{c}{a}$=$\frac{1}{cosθ-sinθ}$=$\frac{1}{\sqrt{2}cos(θ+\frac{π}{4})}$,
∵∠AF1F2∈(0,$\frac{π}{12}$),
∴θ+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{π}{3}$),
∴cos(θ+$\frac{π}{4}$)∈($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),
∴$\sqrt{2}$cos(θ+$\frac{π}{4}$)∈($\frac{\sqrt{2}}{2}$,1),
∴e∈(1,$\sqrt{2}$),
故选:A.
点评 本题考查双曲线的定义与性质,考查三角函数知识,考查学生的计算能力,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
6.曲线y=x2在x=0处的( )
| A. | 切线斜率为1 | B. | 切线方程为y=2x | C. | 没有切线 | D. | 切线方程为y=0 |
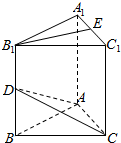 如图在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1,∠BAC=90°,点D,E分别为棱BB1,A1C1的中点,求异面直线B1E、CD所成角的余弦值.
如图在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1,∠BAC=90°,点D,E分别为棱BB1,A1C1的中点,求异面直线B1E、CD所成角的余弦值.