题目内容

在△ABC中，AB=
a
，AC=
b
，过点A作AD⊥BC，交BC于D，若存在实数λ，使得
BD
=λ
BC
，求 λ，用
a
，
b
表示．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，由
BD
=λ
BC
，可得
AD
=
AB
+λ
BC
，由AD⊥BC，可得
AD
•
BC
=(
AB
+λ
BC
)•
BC
=0，又
BC
=
AC
-
AB
，代入展开即可．
解答： 解：如图所示，
∵
BD
=λ
BC
，
∴
AD
=
AB
+λ
BC
，
∵AD⊥BC，
∴
AD
•
BC
=(
AB
+λ
BC
)•
BC
=0，
又
BC
=
AC
-
AB
，
∴
AB
•(
AC
-
AB
)+λ(
AC
-
AB
)2=0，
∴λ=
a
•(
b
-
a
)
(
b
-
a
)2
．
点评：本题考查了向量的三角形法则、向量垂直与数量积的关系，考查了数形结合的方法，属于中档题．
练习册系列答案
相关题目
设椭圆D：
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点分别为F1，F2，上顶点为A，在x轴的负半轴上有一点B，满足
BF1
=
F1F2
，且
AB
•
AF2
=0
（1）若过A，B，F2三点的圆C恰好与直线l：x-
3
y-3=0相切，求圆C的方程及椭圆D的方程；
（2）若过点T（3，0）的直线与椭圆D相交于两点M，N，设P为椭圆上一点，且满足
OM
+
ON
=t•
OP
（O为坐标原点），求实数t的取值范围．
已知函数f（x）=ax2+（2a+1）x+1-3a（a≠0），若f（lgx）=0的两根之积为10，求a的值．
函数f（x）=x2+mln（x+1）．
（1）若函数f（x）是定义域上的单调函数，求实数m的取值范围；
（2）若m=-1，试比较当x∈（0，+∞）时，f（x）与x3的大小；
（3）证明：对任意的正整数n，不等式e0+e-1×4+e-2×9+…+e (1-n)n2＜
n(n+3)
2
成立．
如图，椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F1，右焦点为F2，离心率e=
6
3
，过F1 的直线交椭圆于A，B两点，且△ABF2的周长为4
3
．
（1）求椭圆E的方程；
（2）过点P（0，2）的动直线l与椭圆E相交于C，D两点，O为原点，求△COD面积的最大值．
已知f（x）=ax2+（a+1）x+（a-3），若它的图象过原点，则a=
 
．关于y轴对称，则a=
 
．
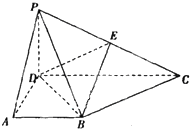在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是直角梯形，AB∥DC，∠ADC=90°，AB=AD=PD=1，CD=2．
（Ⅰ）求证：BC⊥平面PBD；
（Ⅱ）问侧棱PC上是否存在异于端点的一点E，使得二面角E-BD-P的余弦值为
6
3
．若存在，试确定点E的位置；若不存在，说明理由．
如图所示，在边长为
2
的正方形ABCD中，动圆Q的半径为1，圆心在线段CB（含端点）上运动，P是圆Q上及内部的动点，设向量
AP
=m
AB
+n
AD
（m，n为实数），则m+n的取值范围为
 
．
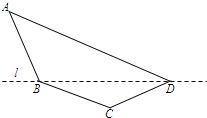某单位设计一上展览沙盘，现谷在沙盘平面内，布设一个对角线在l上的四边形电气线路，如图所示，为充分利用现有材料，边BC，CD用一根5米长的材料弯折而成，边BA，AD用一根9米长的材料弯折而成，要求∠A和∠C互补，且AB=BC．
（1）设AB=x米，cosA=f（x），求f（x）的解析式，并指出x的取值范围；
（2）若四边形ABCD面积为6
3
，且x∈N*，求x的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网