题目内容
已知e为自然对数的底数,则曲线y=xex在点(1,e)处的切线斜率为 .
考点:利用导数研究曲线上某点切线方程
专题:导数的概念及应用
分析:利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
解答:
解:依题意得y′=ex+xex,
因此曲线y=xex在x=1处的切线的斜率等于2e,
故答案为:2e.
因此曲线y=xex在x=1处的切线的斜率等于2e,
故答案为:2e.
点评:本题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
相关题目
已知平面向量
=(2cos2x,sin2x),
=(cos2x,-2sin2x),f(x)=
•
,要得到y=sin2x+
cos2x的图象,只需要将y=f(x)的图象( )
| a |
| b |
| a |
| b |
| 3 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
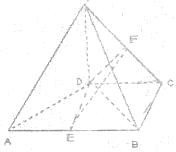 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°. 如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则∠ACB=
如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则∠ACB=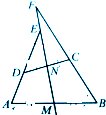 已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证:
已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证: