题目内容
已知函数f(x)=2lnx,g(x)=ax,若存在x0∈[1,e],使得f(x0)<g(x0),则a的取值范围为 .
考点:函数恒成立问题
专题:不等式的解法及应用
分析:把存在x0∈[1,e],使得f(x0)<g(x0)成立转化为f(x)-g(x)=2lnx-ax<0在[1,e]上有解,即a>
在[1,e]上有解,构造函数h(x)=
,利用导数求其最小值得答案.
| 2lnx |
| x |
| 2lnx |
| x |
解答:
解:f(x)=2lnx,g(x)=ax,
若存在x0∈[1,e],使得f(x0)<g(x0),
即f(x)-g(x)=2lnx-ax<0在[1,e]上有解,
即a>
,
令h(x)=
,则h′(x)=
,
当x∈[1,e]时,h′(x)>0,函数h(x)在[1,e]上为增函数,
∴h(x)min=h(1)=0.
∴a的取值范围为[0,+∞).
若存在x0∈[1,e],使得f(x0)<g(x0),
即f(x)-g(x)=2lnx-ax<0在[1,e]上有解,
即a>
| 2lnx |
| x |
令h(x)=
| 2lnx |
| x |
| 2-2lnx |
| x2 |
当x∈[1,e]时,h′(x)>0,函数h(x)在[1,e]上为增函数,
∴h(x)min=h(1)=0.
∴a的取值范围为[0,+∞).
点评:本题考查了函数恒成立问题,考查了数学转化思想方法,训练了利用导数求函数的最值,是中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
已知平面向量
=(2cos2x,sin2x),
=(cos2x,-2sin2x),f(x)=
•
,要得到y=sin2x+
cos2x的图象,只需要将y=f(x)的图象( )
| a |
| b |
| a |
| b |
| 3 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
过边长为2的正方形中心作直线l将正方形分为两个部分,将其中的一个部分沿直线l翻折到另一个部分上.则两个部分图形中不重叠的面积的最大值为( )
| A、2 | ||
B、2(3-
| ||
C、4(2-
| ||
D、4(3-2
|
在数列{an}中,an>0,a1=
,如果an+1是1与
的等比中项,那么a1+
+
+
+…+
的值是( )
| 1 |
| 2 |
| 2anan+1+1 |
| 4-an2 |
| a2 |
| 22 |
| a3 |
| 32 |
| a4 |
| 42 |
| a100 |
| 1002 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,在边长为
如图所示,在边长为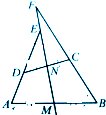 已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证:
已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证: