题目内容
已知凼数f(x)=sin2x+2sinxcosx-cos2x,x∈R,
(1)求凼数f(x)的最小正周期
(2)求凼数f(x)的单调递减区间.
(1)求凼数f(x)的最小正周期
(2)求凼数f(x)的单调递减区间.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(1)首先通过三角函数关系式的恒等变换把函数关系式变形成正弦型函数,进一步求出正弦型函数的周期.
(2)利用(1)求出的函数关系式,进一步利用整体思想求出函数的单调递减区间.
(2)利用(1)求出的函数关系式,进一步利用整体思想求出函数的单调递减区间.
解答:
解:(1)f(x)=sin2x+2sinxcosx-cos2x
=sin2x-cos2x
=
sin(2x-
),
所以:T=
=π;
(2)由于f(x)=
sin(2x-
),
令:
+2kπ≤2x-
≤2kπ+
(k∈Z),
解得:
+kπ≤x≤kπ+
(k∈Z),
所以:函数的单调递减区间为:[
+kπ,kπ+
](k∈Z).
=sin2x-cos2x
=
| 2 |
| π |
| 4 |
所以:T=
| 2π |
| 2 |
(2)由于f(x)=
| 2 |
| π |
| 4 |
令:
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
解得:
| 3π |
| 8 |
| 7π |
| 8 |
所以:函数的单调递减区间为:[
| 3π |
| 8 |
| 7π |
| 8 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数周期公式的应用,正弦型函数单调区间的确定,属于基础题型.

练习册系列答案
相关题目
过边长为2的正方形中心作直线l将正方形分为两个部分,将其中的一个部分沿直线l翻折到另一个部分上.则两个部分图形中不重叠的面积的最大值为( )
| A、2 | ||
B、2(3-
| ||
C、4(2-
| ||
D、4(3-2
|
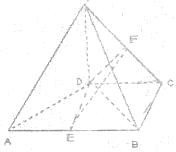 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.