题目内容
已知函数f(x)=|ex-1|,g(x)=
,则F(x)=f(x)-g(x)的零点的个数为( )
|
| A、2 | B、3 | C、4 | D、5 |
考点:根的存在性及根的个数判断,函数零点的判定定理
专题:函数的性质及应用
分析:首先,在同一坐标系中画出函数y=f(x),y=g(x)的图象,然后,判断交点的个数即可.
解答:
解:根据已知,当x≤0时,g(x)=1-|x+1|,当0<x<2时,g(x)=2[1-|x-2+1|]=2(1-|x-1|),
然后去掉绝对值,得到函数g(x)=
的部分图象,
令F(x)=f(x)-g(x)=0,得
f(x)=g(x),
故函数y=f(x)与函数y=g(x)的交点个数就是该方程的根,
如图所示:
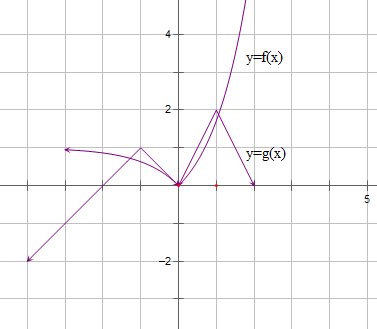
F(x)=f(x)-g(x)的零点的个数为3个.
故选:B.
然后去掉绝对值,得到函数g(x)=
|
令F(x)=f(x)-g(x)=0,得
f(x)=g(x),
故函数y=f(x)与函数y=g(x)的交点个数就是该方程的根,
如图所示:
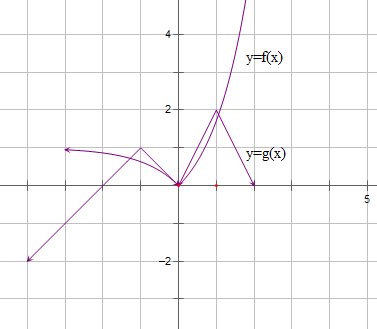
F(x)=f(x)-g(x)的零点的个数为3个.
故选:B.
点评:本题重点考查了函数的零点等知识,属于中档题.

练习册系列答案
相关题目
已知平面向量
=(2cos2x,sin2x),
=(cos2x,-2sin2x),f(x)=
•
,要得到y=sin2x+
cos2x的图象,只需要将y=f(x)的图象( )
| a |
| b |
| a |
| b |
| 3 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
过边长为2的正方形中心作直线l将正方形分为两个部分,将其中的一个部分沿直线l翻折到另一个部分上.则两个部分图形中不重叠的面积的最大值为( )
| A、2 | ||
B、2(3-
| ||
C、4(2-
| ||
D、4(3-2
|
已知抛物线C:y2=4x的焦点为F,过点F的直线l交抛物线于M,N两点,且|MF|=2|NF|,则直线l的斜率为( )
A、±
| ||||
B、±2
| ||||
C、±
| ||||
D、±
|
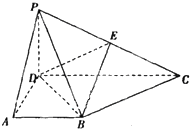 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2. 如图所示,在边长为
如图所示,在边长为