题目内容
设A为△ABC内角，满足sinA+cosA=a，当-1＜a＜0时，则△ABC是 三角形．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由条件可得可得 sinA＞0，cosA＜0，故 A为钝角，可得△ABC是钝角三角形．
解答：
解：∵A为△ABC内角，满足sinA+cosA=a，当-1＜a＜0时，可得 sinA＞0，cosA＜0，
∴A为钝角，∴△ABC是钝角三角形，
故答案为：钝角．
∴A为钝角，∴△ABC是钝角三角形，
故答案为：钝角．
点评：本题主要考查正弦函数、余弦函数在（0，π）上的符号，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
函数y=2-
的值域是（ ）
| -x2+4x |
| A、[-2，2] | ||||
| B、[1，2] | ||||
| C、[0，2] | ||||
D、[-
|
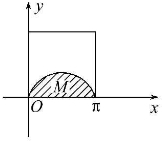如图，在边长为π的正方形内的正弦曲线y=sinx与x轴围成的区域记为M（图中阴影部分），随机往正方形内投一个点P，则点P落在区域M内的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知AB为圆O的一条弦，且|AB|=2，则数量积
•
的值为（ ）
| AB |
| AO |
| A、2 | B、3 |
| C、4 | D、与圆的半径有关 |