题目内容
设函数y=f(x)是定义在R上的函数,并且满足下面三个条件:(1)f(x)在R上是减函数;(2)f(xy)=f(x)+f(y);(3)f(3)=-1.
(1)求f(1)和f(
)的值;
(2)解不等式f(x)+f(x-
)<2.
(1)求f(1)和f(
| 1 |
| 3 |
(2)解不等式f(x)+f(x-
| 8 |
| 9 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)令x=y=1,x=3,y=
,即可求得f(1)、f(
)的值;
(2)根据函数的单调性把函数值不等式转化为自变量不等式,解不等式即可求得结果.
| 1 |
| 3 |
| 1 |
| 3 |
(2)根据函数的单调性把函数值不等式转化为自变量不等式,解不等式即可求得结果.
解答:
解:(1)I)∵函数y=f(x)是定义在(0,+∞)上的函数,
对正数x、y都有f(xy)=f(x)+f(y),
令x=y=1,
则 f(1×1)=f(1)+f(1),
∴f(1)=0.
令x=3,y=
,∴f(3×
)=f(3)+f(
)
∴f(1)=f(3)+f(
)
又∵f(3)=-1,
∴f(
)=1;
(2)令x=y=
则f(
×
)=f(
)+f(
),
∴f(
)=1+1=2
∵f(x)+f(x-
)<2.
∴f[x(x-
)]<f(
),
又∵f(x)在R上是单调增函数,
∴x(x-
)>(
)
解得x>1或x<
.
∴原不等式的解集为{x|x>1或x<
}.
对正数x、y都有f(xy)=f(x)+f(y),
令x=y=1,
则 f(1×1)=f(1)+f(1),
∴f(1)=0.
令x=3,y=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴f(1)=f(3)+f(
| 1 |
| 3 |
又∵f(3)=-1,
∴f(
| 1 |
| 3 |
(2)令x=y=
| 1 |
| 3 |
则f(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴f(
| 1 |
| 9 |
∵f(x)+f(x-
| 8 |
| 9 |
∴f[x(x-
| 8 |
| 9 |
| 1 |
| 9 |
又∵f(x)在R上是单调增函数,
∴x(x-
| 8 |
| 9 |
| 1 |
| 9 |
解得x>1或x<
| 1 |
| 9 |
∴原不等式的解集为{x|x>1或x<
| 1 |
| 9 |
点评:考查利用函数单调性的定义探讨抽象函数的单调性问题,对于解决抽象函数的一般采用赋值法,求某些点的函数值和证明不等式等,体现了转化的思想.

练习册系列答案
相关题目
函数f(x)=x-
的零点所在的大致区间是( )
| 2 |
| x |
| A、(-4,-2) |
| B、(-2,-1) |
| C、(2,4) |
| D、(4,+∞) |
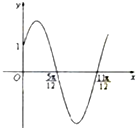 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<