题目内容
求f(x)=sin(2x-
)在[0,
]上的最大值和最小值.
| π |
| 6 |
| π |
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由条件利用正弦函数的定义域和值域,求得f(x)=sin(2x-
)在[0,
]上的最大值和最小值.
| π |
| 6 |
| π |
| 2 |
解答:
解:由x∈[0,
],可得2x-
∈[-
,
],故当2x-
=
时,函数取得最大值为1;
当2x-
=-
时,函数取得最小值为-
.
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 2 |
当2x-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
点评:本题主要考查正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
设f(x)=x(x-1)(x-2)…(x-2015),则f′(2015)=( )
| A、-2013! |
| B、-2015! |
| C、2013! |
| D、2015! |
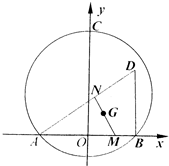 在平面直角坐标系xOy中,已知点A(-1,0),B(1,0),C(0,a)(a∈R且a≠0),且动点D满足DA=
在平面直角坐标系xOy中,已知点A(-1,0),B(1,0),C(0,a)(a∈R且a≠0),且动点D满足DA=