题目内容
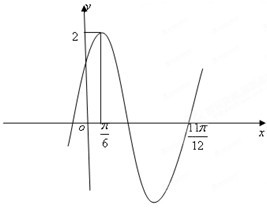 已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<
已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<| π |
| 2 |
(1)求函数f(x)的解析式;写出函数取得最小值时的x取值集合;
(2)求函数f(x)的单调增区间;
(3)若f(x)-2≤m≤f(x)+3在x∈[-
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:综合题
分析:第(1)问根据图象易得A和周期,进而求出ω,φ值要代入一个点的坐标求解;
第(2)问根据正弦函数的单调区间求解;
第(3)要把恒成立问题转化成最大值最小值问题解决.
第(2)问根据正弦函数的单调区间求解;
第(3)要把恒成立问题转化成最大值最小值问题解决.
解答:
解:(1)结合给出的三角函数的形式与图象,可知A=2,
T=
-
=
,
由
=
得,ω=2,
∴f(x)=2sin(2x+φ),代入点(
,2)得2sin(2×
+φ)=2,
∴
+φ=
+2kπ,k∈Z.
又∵|φ|<
,∴Φ=
,
∴f(x)=2sin(2x+
);
当函数f(x)=2sin(2x+
)取得最小值时,2x+
=-
+2kπ,k∈Z.
解得x=
+kπ,k∈Z,
∴函数f(x)取得最小值时的x取值集合为{x|x=
+kπ,k∈Z}
(2)由-
+2kπ≤2x+
≤
+2kπ,k∈Z,解得:-
+kπ≤x≤
+kπ,k∈Z,
∴函数f(x)的单调增区间是[-
+kπ,
+kπ],k∈Z.
(3)∵f(x)-2≤m≤f(x)+3在x∈[-
,0]上恒成立,
∴m要大于f(x)-2的最大值,要小于f(x)+3的最小值,
又∵函数f(x)=2sin(2x+
)在x∈[-
,0]上的最大值为1,最小值为-2,
∴f(x)-2的最大值为-1,f(x)+3的最小值为1,
∴-1≤m≤1.
| 3 |
| 4 |
| 11π |
| 12 |
| π |
| 6 |
| 3π |
| 4 |
由
| 2π |
| ω |
| 3π |
| 4 |
∴f(x)=2sin(2x+φ),代入点(
| π |
| 6 |
| π |
| 6 |
∴
| π |
| 3 |
| π |
| 2 |
又∵|φ|<
| π |
| 2 |
| π |
| 6 |
∴f(x)=2sin(2x+
| π |
| 6 |
当函数f(x)=2sin(2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解得x=
| π |
| 3 |
∴函数f(x)取得最小值时的x取值集合为{x|x=
| π |
| 3 |
(2)由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴函数f(x)的单调增区间是[-
| π |
| 3 |
| π |
| 6 |
(3)∵f(x)-2≤m≤f(x)+3在x∈[-
| π |
| 2 |
∴m要大于f(x)-2的最大值,要小于f(x)+3的最小值,
又∵函数f(x)=2sin(2x+
| π |
| 6 |
| π |
| 2 |
∴f(x)-2的最大值为-1,f(x)+3的最小值为1,
∴-1≤m≤1.
点评:本题是三角函数的综合性的题目,考查了根据图象求解析式、正弦型函数的单调区间、最值的求法,考查了数形结合、转化与化归的数学思想.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
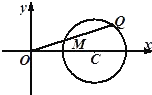 (理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点.
(理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点. 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AB⊥AD,平面PAD⊥平面ABCD,若AB=8,DC=2,AD=6
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AB⊥AD,平面PAD⊥平面ABCD,若AB=8,DC=2,AD=6