题目内容
我们定义函数y=[x]([x]表示不大于x的最大整数)为“下整函数”;定义y={x}({x}表示不小于x的最小整数)为“上整函数”;例如[4.3]=4,[5]=5;{4.3}=5,{5}=5.某停车场收费标准为每小时2元,即不超过1小时(包括1小时)收费2元,超过一小时,不超过2小时(包括2小时)收费4元,以此类推.若李刚停车时间为x小时,则李刚应缴费为(单位:元)( )
| A、2[x+1] |
| B、2([x]+1) |
| C、2{x} |
| D、{2x} |
考点:分段函数的应用
专题:计算题,应用题,函数的性质及应用
分析:根据收费规则,计算缴费应该用上整函数好一些,李刚应缴费为2{x}.
解答:
解:根据收费规则,
即不超过1小时(包括1小时)收费2元,超过一小时,不超过2小时(包括2小时)收费4元,以此类推,
故计算缴费应该用上整函数好一些,
则由题意知,
李刚应缴费为2{x};
若x=1,则2[x+1]=4,故A不正确;
若x=1,则2([x]+1)=4,故B不正确;
若x=1.5,则{2x}=3,故D不正确;
故选C.
即不超过1小时(包括1小时)收费2元,超过一小时,不超过2小时(包括2小时)收费4元,以此类推,
故计算缴费应该用上整函数好一些,
则由题意知,
李刚应缴费为2{x};
若x=1,则2[x+1]=4,故A不正确;
若x=1,则2([x]+1)=4,故B不正确;
若x=1.5,则{2x}=3,故D不正确;
故选C.
点评:本题考查了分段函数在实际问题中的应用,属于基础题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知△ABC三个顶点的坐标分别为A(0,0),B(2,2),C(0,c),若
⊥
,那么c的值是( )
| AB |
| BC |
| A、-1 | B、3 | C、-3 | D、4 |
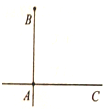 如图,两高速公路线垂直相交于站A,若已知AB=100千米,甲汽车从A站出发,沿AC方向以50千米/小时的速度行驶,同时乙汽车从B站出发,一年BA方向以v千米/小时的速度行驶,至A站即停止前行(甲车仍继续行驶)(两车的车长忽略不计).
如图,两高速公路线垂直相交于站A,若已知AB=100千米,甲汽车从A站出发,沿AC方向以50千米/小时的速度行驶,同时乙汽车从B站出发,一年BA方向以v千米/小时的速度行驶,至A站即停止前行(甲车仍继续行驶)(两车的车长忽略不计).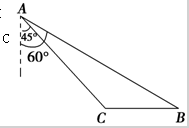 如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(