已知在平面直角坐标系xOy上的区域D由不等式组1≤x≤2y≤2x≤2y给定．若M(x.y)为D上的动点.点A的坐标为(2.1).则z=OA•AM的最大值为( ) A.-5B.-1C.1D.0 题目和参考答案——青夏教育精英家教网—

题目内容

已知在平面直角坐标系xOy上的区域D由不等式组

1≤x≤2

y≤2

x≤2y

给定．若M（x，y）为D上的动点，点A的坐标为（2，1），则z=

•

的最大值为（　　）

A、-5

B、-1

C、1

D、0

考点：平面向量数量积的运算,简单线性规划

专题：平面向量及应用

分析：先画出平面区域D，进行数量积的运算即得z=2x+y-5，所以y=-2x+5+z，所以根据线性规划的方法求出z的最大值即可．

解答： 解：D所表示的区域如图中阴影部分所示，

•

=（2，1）•（x-2，y-1）=2x+y-5；
∴y=-2x+5+z；
∴5+z表示直线y=-2x+5+z在y轴上的截距，所以截距最大时z最大；
如图所示，当该直线经过点（2，2）时，截距最大，此时z最大；
所以点（2，2）带人直线y=-2x+5+z即得z=1．
故选C．

点评：考查不等式组表示一个平面区域，并能找到这个平面区域，根据点的坐标求向量的坐标，以及向量数量积的坐标运算，直线在y轴上的截距，线性规划的方法求最值．

练习册系列答案

=（-3λ，2），定点A（3，0），其中0＜λ＜1．一自点A发出的光线以

为方向向量射到y轴的B点处，并被y轴反射，其反射光线与自点A以

为方向向量的光线相交于点P．
（1）求点P的轨迹方程；
（2）问A、B、P、O四点能否共圆（O为坐标原点），并说明理由．

我市某镇的一种特产由于运输原因，长期只能在当地销售．当地政府对该特产的销售投资收益为：每投入x万元，可获得利润P=-

100

（x-60）2+41（万元）．当地政府拟在“十二•五”规划中加快开发该特产的销售，其规划方案为：在规划前后对该项目每年最多可投入100万元的销售投资，在实施规划5年的前两年中，每年都从100万元中拨出50万元用于修建一条公路，两年修成，通车前该特产只能在当地销售；公路通车后的3年中，该特产既在本地销售，也在外地销售．在外地销售的投资收益为：每投入x万元，可获利润Q=-

100

（100-x）2+

294

（100-x）+160（万元）．
（1）若不进行开发，求5年所获利润的最大值是多少？
（2）若按规划实施，求5年所获利润（扣除修路后）的最大值是多少？
（3）根据（1），（2），该方案是否具有实施价值？

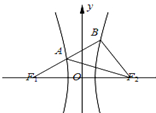如图，F₁，F₂是双曲线C：

=1（a＞0，b＞0）的左、右焦点，过F₁的直线l与C的左、右两支分别交于A，B两点．若△ABF₂为等边三角形，则双曲线的离心率为（　　）

设数列{a_n}中，首项a₁=1，点（a_n，a_n+1）（n=1，2，3，…）均在直线y=2x+1上
（1）求a₂，a₃，a₄的值；
（2）求数列{a_n}的通项公式．

我们定义函数y=[x]（[x]表示不大于x的最大整数）为“下整函数”；定义y={x}（{x}表示不小于x的最小整数）为“上整函数”；例如[4.3]=4，[5]=5；{4.3}=5，{5}=5．某停车场收费标准为每小时2元，即不超过1小时（包括1小时）收费2元，超过一小时，不超过2小时（包括2小时）收费4元，以此类推．若李刚停车时间为x小时，则李刚应缴费为（单位：元）（　　）

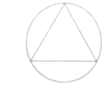某人随机地向如图所示的正三角形及其外接圆区域内部设计（不包括三角形及其外接圆的边界），则针孔到正三角形内部（不包括边界）的概率为（　　）

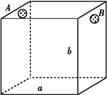为处理含有某种杂质的污水，要制造一个底宽为2米的无盖长方体沉淀箱（如图），污水从A孔流入，经沉淀后从B孔流出，设箱体的长度为a米，高度为b米，已知流出的水中该杂质的质量分数与a、b的乘积ab成反比，现有制箱材料60平方米，当a、b各为（　　）米时，经沉淀后流出的水中该杂质的质量分数最小（A、B孔的面积忽略不计）？

试题分类