题目内容

已知△ABC三个顶点的坐标分别为A（0，0），B（2，2），C（0，c），若
AB
⊥
BC
，那么c的值是（　　）
A、-1B、3C、-3D、4
考点：平面向量数量积的运算
专题：平面向量及应用
分析：先求出
AB
，
BC
，根据
AB
⊥
BC
，便有
AB
•
BC
=0，进行数量积的运算即可求出c．
解答： 解：
AB
=(2，2)，
BC
=(-2，c-2)；
∵
AB
⊥
BC
；
∴
AB
•
BC
=-4+2C-4=0；
∴c=4．
故选D．
点评：考查两非零向量垂直的充要条件，以及向量数量积的坐标运算．
练习册系列答案
相关题目
-
π
12
弧度角在第
 
象限．
我市某镇的一种特产由于运输原因，长期只能在当地销售．当地政府对该特产的销售投资收益为：每投入x万元，可获得利润P=-
1
100
（x-60）2+41（万元）．当地政府拟在“十二•五”规划中加快开发该特产的销售，其规划方案为：在规划前后对该项目每年最多可投入100万元的销售投资，在实施规划5年的前两年中，每年都从100万元中拨出50万元用于修建一条公路，两年修成，通车前该特产只能在当地销售；公路通车后的3年中，该特产既在本地销售，也在外地销售．在外地销售的投资收益为：每投入x万元，可获利润Q=-
99
100
（100-x）2+
294
5
（100-x）+160（万元）．
（1）若不进行开发，求5年所获利润的最大值是多少？
（2）若按规划实施，求5年所获利润（扣除修路后）的最大值是多少？
（3）根据（1），（2），该方案是否具有实施价值？
设数列{an}中，首项a1=1，点（an，an+1）（n=1，2，3，…）均在直线y=2x+1上
（1）求a2，a3，a4的值；
（2）求数列{an}的通项公式．
我们定义函数y=[x]（[x]表示不大于x的最大整数）为“下整函数”；定义y={x}（{x}表示不小于x的最小整数）为“上整函数”；例如[4.3]=4，[5]=5；{4.3}=5，{5}=5．某停车场收费标准为每小时2元，即不超过1小时（包括1小时）收费2元，超过一小时，不超过2小时（包括2小时）收费4元，以此类推．若李刚停车时间为x小时，则李刚应缴费为（单位：元）（　　）
A、2[x+1]
B、2（[x]+1）
C、2{x}
D、{2x}
已知函数f（x）=
1，x是有理数
0，x是无理数
，下列命题是真命题的是
 
（只填命题序号）．
①函数f（x）是偶函数；②对任意x∈R，f（x+
2
）=f（x）；
③对任意x∈R，f（x+2）=f（x）；
④对任意x，y∈R，f（x+y）=
1
2
（f（x）+f（x））；
⑤若存在x，y∈R，使得f（x+y）=f（x）+f（y），则x，y都为无理数．
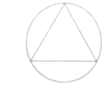某人随机地向如图所示的正三角形及其外接圆区域内部设计（不包括三角形及其外接圆的边界），则针孔到正三角形内部（不包括边界）的概率为（　　）
A、
3
3
2π
B、
3
π
C、
3
3
4π
D、
3
3
5π
已知函数f（x）=x2+2ax+1-a在（-1，1）上有零点，求a的取值范围．
设学生的考试成绩为G，则下面的代码的算法目的是（　　）
A、计算50个学生的平均成绩
B、计算50个学生中不及格的人数
C、计算50个学生中及格的人数
D、计算50个学生的总成绩

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网