题目内容
6.(Ⅰ)求和:an+an-1b+…+abn-1+bn(ab≠0);(Ⅱ)已知an=2n,bn=3n,将数列{an}的各项依次作为数列{cn}的奇数项,将数列b{an}的各项依次作为数列{cn}的偶数项,求数列{cn}的通项公式;
(Ⅲ)数列{an}满足a1=2,$\sum_{i=1}^n{i{a_i}=4-\frac{n+2}{{{2^{n-1}}}}}$(n≥2),求数列{an}的通项公式.
分析 (Ⅰ)分a=b和a≠b,借助于等差数列和等比数列的求和公式求解;
(Ⅱ)由题意,数列{cn}的奇数项构成以2为首项,以2为公差的等差数列;偶数项构成以3为首项,以3为公比的等比数列.然后分别写出通项公式;
(Ⅲ)由已知递推式写出(n-1)时的递推式,两式作差得答案.
解答 解:(Ⅰ)当a=b时,
an+an-1b+…+abn-1+bn=(n+1)an;
当a≠b时,
an+an-1b+…+abn-1+bn(ab≠0)
=$\frac{{a}^{n}[1-(\frac{b}{a})^{n+1}]}{1-\frac{b}{a}}=\frac{{a}^{n+1}-{b}^{n+1}}{a-b}$;
(Ⅱ)由题意,数列{cn}的奇数项构成以2为首项,以2为公差的等差数列;
偶数项构成以3为首项,以3为公比的等比数列.
则{cn}的通项公式为:${c}_{n}=\left\{\begin{array}{l}{4n-2,(n为奇数)}\\{{3}^{2n},(n为偶数)}\end{array}\right.$;
(Ⅲ)由${a_1}=2,\sum_{i=1}^n{i{a_i}=4-\frac{n+2}{{{2^{n-1}}}}}(n≥2)$,
得:$1•{a}_{1}+2•{a}_{2}+3•{a}_{3}+…n{a}_{n}=4-\frac{n+2}{{2}^{n-1}}$,
∴1•a1+2•a2+3•a3+…+(n-1)an-1=$4-\frac{n+1}{{2}^{n-2}}$(n≥2).
则$n{a}_{n}=4-\frac{n+2}{{2}^{n-1}}-4+\frac{n+1}{{2}^{n-2}}$=$\frac{n}{{2}^{n-1}}$,
∴${a}_{n}=\frac{1}{{2}^{n-1}}$(n≥2),
验证a1=2不适合上式,
∴${a}_{n}=\left\{\begin{array}{l}{2,n=1}\\{\frac{1}{{2}^{n-1}},n≥2}\end{array}\right.$.
点评 本题考查数列递推式,考查了等比数列的前n项和公式,训练了作差法求数列的通项公式,是中档题.

| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (-2,1) | B. | [-2,1] | C. | (0,1) | D. | (0,1] |
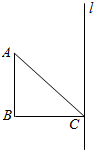 如图,三角形ABC是等腰直角三角形,∠B=90°,AB=1,直线l经过点C且与AB平行,将三角形ABC绕直线l旋转一周得到一个几何体.
如图,三角形ABC是等腰直角三角形,∠B=90°,AB=1,直线l经过点C且与AB平行,将三角形ABC绕直线l旋转一周得到一个几何体.