题目内容
18．函数y=$\frac{{\sqrt{-{x^2}-x+2}}}{lnx}$的定义域为（ ）| A． | （-2，1） | B． | [-2，1] | C． | （0，1） | D． | （0，1] |
分析 根据二次根式的性质结合对数函数的性质得到关于x的不等式组，解出即可．
解答 解：由题意得：
$\left\{\begin{array}{l}{{-x}^{2}-x+2≥0}\\{x＞0且lnx≠0}\end{array}\right.$，
解得：0＜x＜1，
故选：C．
点评 本题考察了求函数的定义域问题，考察二次根式的性质以及对数函数的性质，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
3．
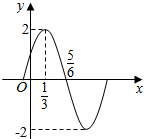已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为（ ）| A． | f（x）=2sin（πx+$\frac{π}{6}$） | B． | f（x）=2sin（πx+$\frac{π}{3}$） | C． | $f（x）=2sin（{2πx-\frac{π}{6}}）$ | D． | y=2sin（πx-$\frac{π}{6}$） |
7．棱长为2的正四面体的表面积是（ ）
| A． | 4$\sqrt{3}$ | B． | 4 | C． | $\sqrt{3}$ | D． | 16 |