题目内容
17.已知命题P:x1,x2是方程x2-mx-1=0的两个实根,且不等式a2+4a-3≤|x1-x2|对任意m∈R恒成立;命题q:不等式ax2+2x-1>0有解,若命题p∨q为真,p∧q为假,求实数a的取值范围.分析 化简命题p,q;由p∨q为真命题,p∧q为假命题知p与q有且仅有一个为真.从而得出a的取值范围.
解答 解:∵x1,x2是方程x2-mx-1=0的两个实根,
∴x1+x2=m,x1•x2=-1,
|x1-x2|=$\sqrt{{m}^{2}+4}$,
∴当m∈R时,|x1-x2|min=2.
由不等式a2+4a-3≤|x1-x2|对任意m∈R恒成立,
得:a2+4a-5≤0,
∴-5≤a≤1;
∴命题p为真命题时-5≤a≤1.
命题p为假命题时a>1或a<-5;
命题q:不等式ax2+2x-1>0有解,
①当a>0时,显然有解,
②当a=0时,2x-1>0有解,
③当a<0时,∵ax2+2x-1>0有解,
∴△=4+4a>0,∴-1<a<0;
从而命题p:不等式ax2+2x-1>0有解时a>-1
∴命题q是真命题时a>-1,命题q是假命题时a≤-1.
∵p∨q真,p∧q假,
∴p与q有且仅有一个为真.
(1)当命题p是真命题且命题q是假命题时-5≤a≤-1;
(2)当命题p是假命题且命题q是真命题时a>1;
综上所述:a的取值范围为:-5≤a≤-1或a>1.
点评 本题考查了复合命题真假性的判断、方程的解的判断、韦达定理及分类讨论的思想,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
5.已知一个等比数列首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的公比和项数分别为( )
| A. | 8,2 | B. | 2,4 | C. | 4,10 | D. | 2,8 |
12.设集合A=$\left\{{x|y=\sqrt{x-1}}\right\}$,集合B=$\left\{{y|y={{log}_2}x,x∈[{\frac{1}{2},4}]}\right\}$,则A∩B=( )
| A. | (1,2) | B. | [1,2] | C. | [1,2) | D. | (1,2] |
2.圆心为(1,2),且与y轴相切的圆的方程是( )
| A. | (x+1)2+(y+2)2=4 | B. | (x-1)2+(y-2)2=4 | C. | (x+1)2+(y+2)2=1 | D. | (x-1)2+(y-2)2=1 |
7.棱长为2的正四面体的表面积是( )
| A. | 4$\sqrt{3}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 16 |
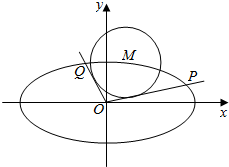 如图,在平面直角坐标系xOy中,设点M(x0,y0)是椭圆C:$\frac{{x}^{2}}{4}$+y2=1上一点,从原点O向圆M:(x-x0)2+(y-y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1,k2
如图,在平面直角坐标系xOy中,设点M(x0,y0)是椭圆C:$\frac{{x}^{2}}{4}$+y2=1上一点,从原点O向圆M:(x-x0)2+(y-y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1,k2