题目内容

14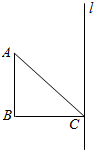．如图，三角形ABC是等腰直角三角形，∠B=90°，AB=1，直线l经过点C且与AB平行，将三角形ABC绕直线l旋转一周得到一个几何体．
（1）求几何体的表面积；
（2）求几何体的体积．

分析 旋转后的几何体为一个圆柱挖去一个圆锥后剩下的几何体．

解答 解：旋转以后的几何体是一个圆柱挖去一个圆锥后剩下的几何体．
圆柱和圆锥的底面半径均为1，高均为1，圆锥的母线长为$\sqrt{2}$．
（1）S=S圆柱底+S圆柱侧+S圆锥侧=π×12+2π×1×1+$π×1×\sqrt{2}$=（3+$\sqrt{2}$）π．
（2）V=V圆柱-V圆锥=π×12×1-$\frac{1}{3}π×{1}^{2}×1$=$\frac{2π}{3}$．

点评 本题考查了旋转体的表面积与体积，分析旋转后所得到的几何体特征是解题关键．

练习册系列答案
相关题目
19．已知0＜β＜α＜$\frac{π}{4}$，cos（α-β）=$\frac{12}{13}$，sin（α+β）=$\frac{3}{5}$，求sin2α的值．
5．已知一个等比数列首项为1，项数是偶数，其奇数项之和为85，偶数项之和为170，则这个数列的公比和项数分别为（　　）
A．8，2B．2，4C．4，10D．2，8
2．圆心为（1，2），且与y轴相切的圆的方程是（　　）
A．（x+1）2+（y+2）2=4B．（x-1）2+（y-2）2=4C．（x+1）2+（y+2）2=1D．（x-1）2+（y-2）2=1
9．已知某校有甲乙两个兴趣小组，其中甲组有2名男生、3名女生，乙组有3名男生，1名女生，学校计划从两兴趣小组中随机各选2名成员参加某项活动．
（1）求选出的4名选手中恰好有一名女生的选派方法数；
（2）记X为选出的4名选手中女选手的人数，求X的概率分布和数学期望．
19．已知点C为线段AB上一点，P为直线AB外一点，PC是∠APB角的平分线，I为PC上一点，满足$\overrightarrow{BI}$=$\overrightarrow{BA}$+λ（$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$+$\frac{\overrightarrow{AP}}{|\overrightarrow{AP}|}$）（λ＞0），$|\overrightarrow{PA}|-|\overrightarrow{PB}|=4$，$|\overrightarrow{PA}-\overrightarrow{PB}|=10$，则$\frac{{\overrightarrow{BI}•\overrightarrow{BA}}}{{|\overrightarrow{BA}|}}$的值为（　　）
A．2B．3C．4D．5
6．（Ⅰ）求和：an+an-1b+…+abn-1+bn（ab≠0）；
（Ⅱ）已知an=2n，bn=3n，将数列{an}的各项依次作为数列{cn}的奇数项，将数列b{an}的各项依次作为数列{cn}的偶数项，求数列{cn}的通项公式；
（Ⅲ）数列{an}满足a1=2，$\sum_{i=1}^n{i{a_i}=4-\frac{n+2}{{{2^{n-1}}}}}$（n≥2），求数列{an}的通项公式．
3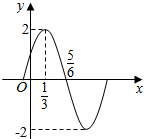．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为（　　）
A．f（x）=2sin（πx+$\frac{π}{6}$）B．f（x）=2sin（πx+$\frac{π}{3}$）C．$f（x）=2sin（{2πx-\frac{π}{6}}）$D．y=2sin（πx-$\frac{π}{6}$）
4．在由一组样本数据（x1，y1），（x2，y2），…，（xn，yn）（n≥2，x1，x2，…，xn不全相等）的点所构成的散点图中，若所有样本点（xi，yi）（i=1，2，…，n）都在直线y=-2x+1上，则这组样本数据中变量x，y的相关系数为（　　）
A．-2B．-1C．1D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网