题目内容
某市质监部门对市场上奶粉进行质量抽检,现将9个进口品牌奶粉的样品编号为1,2,3,4,…,9;6个国产品牌奶粉的样品编号为10,11,12,…,15,按进口品牌及国产品牌分层进行分层抽样,从其中抽取5个样品进行首轮检验,用P(i,j)表示编号为i,j(1≤i<j≤15)的样品首轮同时被抽到的概率.
(Ⅰ)求P(1,15)的值;
(Ⅱ)求所有的P(i,j)(1≤i<j≤15)的和.
(Ⅰ)求P(1,15)的值;
(Ⅱ)求所有的P(i,j)(1≤i<j≤15)的和.
考点:排列、组合及简单计数问题,收集数据的方法,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)由分层抽样的方法从洋奶粉样品中抽取3个,国产奶粉样品中抽取2个,计算出P(1,15)的值;
(Ⅱ)分情况求出1≤i<j≤9,10≤i<j≤15和1≤i≤9<j≤15时,P(i,j)的个数是多少,从而求出它们的和.
(Ⅱ)分情况求出1≤i<j≤9,10≤i<j≤15和1≤i≤9<j≤15时,P(i,j)的个数是多少,从而求出它们的和.
解答:
解:(Ⅰ)由分层抽样可知:
首轮检验从编号为1,2,3,…,9的洋品牌奶粉的样品中抽取3个,
从编号为10,11,…,15的国产品牌奶粉的样品中抽取2个,
∴P(1,15)=
•
=
;
(Ⅱ)①当1≤i<j≤9时,P(i,j)=
=
,
而这样的P(i,j)有
=36个;
②当10≤i<j≤15时,P(i,j)=
=
,
而这样的P(i,j)有
=15个;
③当1≤i≤9<j≤15时,P(i,j)=
•
=
,
而这样的P(i,j)有
•
=54个;
所以,所有的P(i,j)(1≤i<j≤15)的和为
×36+
×15+
×54=10.
首轮检验从编号为1,2,3,…,9的洋品牌奶粉的样品中抽取3个,
从编号为10,11,…,15的国产品牌奶粉的样品中抽取2个,
∴P(1,15)=
| ||
|
| ||
|
| 1 |
| 9 |
(Ⅱ)①当1≤i<j≤9时,P(i,j)=
| ||
|
| 1 |
| 12 |
而这样的P(i,j)有
| C | 2 9 |
②当10≤i<j≤15时,P(i,j)=
| 1 | ||
|
| 1 |
| 15 |
而这样的P(i,j)有
| C | 2 6 |
③当1≤i≤9<j≤15时,P(i,j)=
| ||
|
| ||
|
| 1 |
| 9 |
而这样的P(i,j)有
| C | 1 9 |
| C | 1 6 |
所以,所有的P(i,j)(1≤i<j≤15)的和为
| 1 |
| 12 |
| 1 |
| 15 |
| 1 |
| 9 |
点评:本题考查了分层抽样法的应用以及概率与数学期望的问题,解题的关键是理解题中P(i,j)的含义,以及(Ⅱ)中i、j的适当分情况计算问题,是易错题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
下列命题中,真命题是( )
| A、存在一个△ABC,使a2=b2+c2-3bccosA(a,b,c是三边长,a是内角A的对边) |
| B、?x∈(1,+∞),log0.5x>0 |
| C、幂函数 f(x)=(m-1)xm-3在定义域上是减函数 |
| D、a>1,b>1是ab>1的必要条件 |
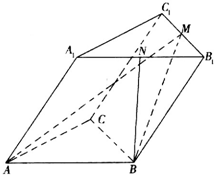 如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.
如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.