题目内容
已知函数f(x)为奇函数,且当x>0时f(x)=x2-2x,若关于x的方程f(x)=a有且仅有2个解,则实数a等于 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据已知结合奇函数的图象关于原点对称,画出函数f(x)的图象,数形结合可得满足条件的a值.
解答:
解:∵函数f(x)为奇函数,
∴函数f(x)的图象关于原点对称,
又∵当x>0时f(x)=x2-2x,
∴函数f(x)的图象如下图所示:

由图可知:若关于x的方程f(x)=a有且仅有2个解,
则实数a=±1
故答案为:±1
∴函数f(x)的图象关于原点对称,
又∵当x>0时f(x)=x2-2x,
∴函数f(x)的图象如下图所示:

由图可知:若关于x的方程f(x)=a有且仅有2个解,
则实数a=±1
故答案为:±1
点评:本题考查的知识点是函数的奇偶性的性质,图象法确定方程的根的个数,其中根据奇函数的图象关于原点对称,画出函数f(x)的图象,是解答的关键.

练习册系列答案
相关题目
已知x,y满足
,且目标函数z=2x+y的最大值是最小值的8倍,则实数a的值是( )
|
| A、1 | ||
B、
| ||
C、
| ||
D、
|
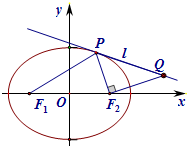 在平面直角坐标系xoy中,已知F1,F2分别是椭圆G:
在平面直角坐标系xoy中,已知F1,F2分别是椭圆G: 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是