题目内容
4.已知等差数列{an}的前n项和Sn满足:S5=30,S10=110,数列{bn}的前n项和Tn满足:Tn=$\frac{3}{2}$bn-$\frac{1}{2}$(n∈N*).(1)求Sn与bn;
(2)比较Snbn与Tnan的大小,并说明理由.
分析 (1)由等差数列前n项和公式列出方程组求出首项与公差,由此能求出差数列{an}的前n项和Sn;由${b}_{n}=\left\{\begin{array}{l}{{T}_{n},n=1}\\{{T}_{n}-{T}_{n-1},n≥2}\end{array}\right.$,能求出数列{bn}的通项公式.
(2)推导出Snbn=(n2+n)•3n-1,Tnan=n•(3n-1),利用作差法能比较Snbn与Tnan的大小.
解答 解:(1)设等差数列{an}的首项为a1,公差为d,
∵差数列{an}的前n项和Sn满足:S5=30,S10=110,
∴$\left\{\begin{array}{l}{5{a}_{1}+\frac{5×4}{2}d=30}\\{10{a}_{1}+\frac{10×9}{2}d=110}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=2}\\{d=2}\end{array}\right.$,
∴an=2+(n-1)×2=2n,
Sn=$\frac{n(2+2n)}{2}$=n2+n.…(3分)
∵数列{bn}的前n项和Tn满足:Tn=$\frac{3}{2}$bn-$\frac{1}{2}$(n∈N*),
∴${b}_{1}={T}_{1}=\frac{3}{2}{b}_{1}-\frac{1}{2}$,解得b1=1,
又${T}_{n+1}=\frac{3}{2}{b}_{n+1}-\frac{1}{2}$,n∈N*,
∴Tn+1-Tn=$\frac{3}{2}{b}_{n+1}-\frac{1}{2}-(\frac{3}{2}{b}_{n}-\frac{1}{2})$=$\frac{3}{2}{b}_{n+1}-\frac{3}{2}{b}_{n}$,n∈N*,
即${b}_{n+1}=\frac{3}{2}{b}_{n+1}-\frac{3}{2}{b}_{n}$,n∈N*,
整理得bn+1=3bn,即$\frac{{b}_{n+1}}{{b}_{n}}$=3(常数),
∴数列{bn}是以1为首项,3为公比的等比数列,
∴bn=3n-1. …(7分)
(2)∵Tn=$\frac{3}{2}$bn-$\frac{1}{2}$=$\frac{{3}^{n}-1}{2}$,
∴Snbn=(n2+n)•3n-1,Tnan=n•(3n-1),
于是Snbn-Tnan=(n2+n)•3n-1-n•(3n-1)=n[3n-1(n-2)+1],…(9分)
当n=1时,Snbn-Tnan=0,即Snbn=Tnan;
当n≥2(n∈N*)时,Snbn-Tnan>0,即Snbn>Tnan.
∴综上,当n=1时,Snbn=Tnan;当n≥2(n∈N*)时,Snbn>Tnan.…(12分)
点评 本题考查数列的前n项和、通项公式的求法,考查两个数的大小的比较,是中档题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

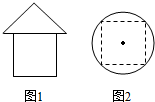 一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )| A. | $2\sqrt{2}π+20$ | B. | $\frac{{2\sqrt{2}π}}{3}+8$ | C. | $({2\sqrt{2}+2})π+16$ | D. | $2\sqrt{2}π+16$ |
| A. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则$\overrightarrow{a}$$⊥\overrightarrow{b}$ | B. | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | ||
| C. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$ | D. | 若存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
| A. | {x|-1<x<4} | B. | {x|-2<x<-1或4<x<5} | C. | {x|x<-1或x>4} | D. | {x|-2<x<5} |
 如图是某建筑物的模型,现在要给该模型进行涂色,有红,黄,蓝,绿四种颜色可用,每层只能用一种颜色,在每一层涂色时,每种颜色被使用的可能性相同.
如图是某建筑物的模型,现在要给该模型进行涂色,有红,黄,蓝,绿四种颜色可用,每层只能用一种颜色,在每一层涂色时,每种颜色被使用的可能性相同.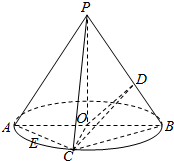 在如图所示的圆锥中,PO是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB上一点,且PO=2,OB=1.
在如图所示的圆锥中,PO是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB上一点,且PO=2,OB=1.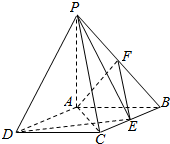 如图:四棱锥P-ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1,$BC=\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图:四棱锥P-ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1,$BC=\sqrt{3}$,点F是PB的中点,点E在边BC上移动.