题目内容
20.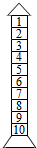 如图是某建筑物的模型,现在要给该模型进行涂色,有红,黄,蓝,绿四种颜色可用,每层只能用一种颜色,在每一层涂色时,每种颜色被使用的可能性相同.
如图是某建筑物的模型,现在要给该模型进行涂色,有红,黄,蓝,绿四种颜色可用,每层只能用一种颜色,在每一层涂色时,每种颜色被使用的可能性相同.(1)求在1至4层中红色恰好被使用1次,黄色没有被使用的概率;
(2)求在1至4层中红色被使用的次数X的分布列和数学期望、方差;
(3)为了使建筑物的色彩绚丽,规定每层只能从上一层未使用的三种颜色中等可能地随机选用一种,已知第1层使用红色,若用Pn表示第n层使用红色的概率,求Pn的表达式,并求出第7层使用红色的概率.
分析 (1)由在1至4层中红色恰好被使用1次,黄色没有被使用,得到前四层中,有一层是红色,其余三层不能是红色和黄色,由此能求出其概率.
(2)由已知得X的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出X的分布列、数学期望和方差.
(3)n=1时,p1=1,n≠1时,pn为n-1层不为红色的前提下第n层为红色,除去第一层和第n层,每层都有3种颜色可以选,由此推导出${p}_{n}-\frac{1}{4}$是等比数列,公比为-$\frac{1}{3}$,首项${p}_{1}-\frac{1}{4}=\frac{3}{4}$,从而能求出Pn的表达式,并求出第7层使用红色的概率.
解答 解:(1)∵在1至4层中红色恰好被使用1次,黄色没有被使用,
∴前四层中,有一层是红色,其余三层不能是红色和黄色,
∴其概率为p=$\frac{{C}_{4}^{1}×{2}^{3}}{{4}^{4}}$=$\frac{1}{8}$.
(2)由已知得X的可能取值为0,1,2,3,4,
P(X=0)=$\frac{{3}^{4}}{{4}^{4}}$=$\frac{81}{256}$,
P(X=1)=$\frac{{C}_{4}^{1}•{3}^{3}}{{4}^{4}}$=$\frac{27}{64}$,
P(X=2)=$\frac{{C}_{4}^{2}•{3}^{2}}{{4}^{4}}$=$\frac{27}{128}$,
P(X=3)=$\frac{{C}_{4}^{3}•3}{{4}^{4}}$=$\frac{3}{64}$,
P(X=4)=$\frac{{C}_{4}^{4}}{{4}^{4}}$=$\frac{1}{256}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{81}{256}$ | $\frac{27}{64}$ | $\frac{27}{128}$ | $\frac{3}{64}$ | $\frac{1}{256}$ |
X的方差D(X)=$(0-1)^{2}×\frac{81}{256}$+(1-1)2×$\frac{27}{64}$+(2-1)2×$\frac{27}{128}$+(3-1)2×$\frac{3}{64}$+(4-1)2×$\frac{1}{256}$=$\frac{3}{4}$.
(3)n=1时,p1=1,
n≠1时,pn为n-1层不为红色的前提下第n层为红色,除去第一层和第n层,每层都有3种颜色可以选,
∴pn=(1-pn-1)×$\frac{{3}^{n-2}}{{3}^{n-1}}$
=$\frac{1}{3}-\frac{1}{3}•{p}_{n-1}$,
pn-$\frac{1}{4}$=-$\frac{1}{3}$(pn-1-$\frac{1}{4}$),
pn-$\frac{1}{4}$=-$\frac{1}{3}$(${p}_{n-1}-\frac{1}{4}$),
∴${p}_{n}-\frac{1}{4}$是等比数列,公比为-$\frac{1}{3}$,首项${p}_{1}-\frac{1}{4}=\frac{3}{4}$,
∴${p}_{n}-\frac{1}{4}$=$\frac{3}{4}×(-\frac{1}{3})^{n-1}$,
∴${p}_{n}=\frac{3}{4}×(-\frac{1}{3})^{n-1}+\frac{1}{4}$,
∴p7=$\frac{3}{4}×(-\frac{1}{3})^{6}+\frac{1}{4}$=$\frac{121}{486}$.
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望、方差的求法,综合性强,难度大,对数学思维能力要求高,解题时要注意等比数列的性质的合理运用.

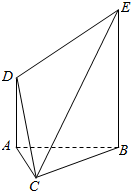 如图,△ABC为等边三角形,D,E是平面ABC同一侧的两点,DA⊥平面ABC,EB⊥平面ABC,EB=2DA.
如图,△ABC为等边三角形,D,E是平面ABC同一侧的两点,DA⊥平面ABC,EB⊥平面ABC,EB=2DA.