题目内容
13.已知直角梯形ABCD,AD∥BC,∠BAD=90°.AD=2,BC=1,P是腰AB上的动点,则$|\overrightarrow{PC}+\overrightarrow{PD}|$的最小值为3.分析 先建立坐标系,以直线AD,AB分别为x,y轴建立平面直角坐标系,设P(0,b)(0≤b≤1),根据向量的坐标运算和模的计算得到,$|\overrightarrow{PC}+\overrightarrow{PD}|$=$\sqrt{9+(1-2b)^{2}}$≥3,问题得以解决.
解答  解:如图,以直线AD,AB分别为x,y轴建立平面直角坐标系,
解:如图,以直线AD,AB分别为x,y轴建立平面直角坐标系,
则A(0,0),B(0,1),C(1,1),D(2,0)
设P(0,b)(0≤b≤1)
则$\overrightarrow{PC}$=(1,1-b),$\overrightarrow{PD}$=(2,-b),
∴$\overrightarrow{PC}$+$\overrightarrow{PD}$=(3,1-2b),
∴$|\overrightarrow{PC}+\overrightarrow{PD}|$=$\sqrt{9+(1-2b)^{2}}$≥3,当且仅当b=$\frac{1}{2}$时取等号,
∴$|\overrightarrow{PC}+\overrightarrow{PD}|$的最小值为3,
故答案为:3.
点评 此题是个基础题.考查向量在几何中的应用,以及向量模的求法,同时考查学生灵活应用知识分析解决问题的能力.

练习册系列答案
相关题目
1.实数x,y满足$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$,则z=|x-y|的最大值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
2.若全集U=R,集合A={x|1<2x<4},B={x|x-1≥0},则A∩∁UB=( )
| A. | {x|1<x<2} | B. | {x|0<x≤1} | C. | {x|0<x<1} | D. | {x|1≤x<2} |
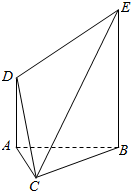 如图,△ABC为等边三角形,D,E是平面ABC同一侧的两点,DA⊥平面ABC,EB⊥平面ABC,EB=2DA.
如图,△ABC为等边三角形,D,E是平面ABC同一侧的两点,DA⊥平面ABC,EB⊥平面ABC,EB=2DA.