题目内容
12.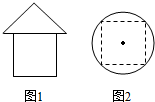 一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )| A. | $2\sqrt{2}π+20$ | B. | $\frac{{2\sqrt{2}π}}{3}+8$ | C. | $({2\sqrt{2}+2})π+16$ | D. | $2\sqrt{2}π+16$ |
分析 由几何体的三视图得这个几何体的上半部分是圆锥,下半部分是正方体,其中正方体的棱长为2,圆锥的母线长l=2,底面半径r=$\sqrt{2}$,由此能求出几何体的表面积.
解答 解:由几何体的三视图得这个几何体的上半部分是圆锥,下半部分是正方体,
其中正方体的棱长为2,圆锥的母线长l=2,底面半径r=$\sqrt{2}$,
∴几何体的表面积为:
S=πrl+5×(22)+πr2-22=$π×2\sqrt{2}+20$=(2$\sqrt{2}+2$)π+16.
故选:C.
点评 本题考查几何体的表面积的求法,是基础题,解题时要认真审题,注意三视图的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.将函数y=sin(x+$\frac{π}{6}$)(x∈R)的图象上所有点的纵坐标不变横坐标缩小到原来的$\frac{1}{2}$,再把图象上各点向左平移$\frac{π}{4}$个单位长度,则所得的图象的解析式为( )
| A. | y=sin(2x+$\frac{5}{6}π$) | B. | y=sin($\frac{1}{2}$x+$\frac{1}{6}$π) | C. | y=sin(2x+$\frac{2}{3}$π) | D. | y=sin($\frac{1}{2}$x+$\frac{5}{12}$π) |
1.实数x,y满足$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$,则z=|x-y|的最大值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
2.若全集U=R,集合A={x|1<2x<4},B={x|x-1≥0},则A∩∁UB=( )
| A. | {x|1<x<2} | B. | {x|0<x≤1} | C. | {x|0<x<1} | D. | {x|1≤x<2} |
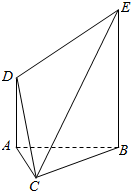 如图,△ABC为等边三角形,D,E是平面ABC同一侧的两点,DA⊥平面ABC,EB⊥平面ABC,EB=2DA.
如图,△ABC为等边三角形,D,E是平面ABC同一侧的两点,DA⊥平面ABC,EB⊥平面ABC,EB=2DA.