题目内容
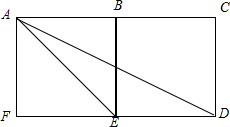如图所示，四边形ABEF和BCDE均是边长为1的正方形，在以A、B、C、D、E、F为起点和终点的向量中．（1）写出与
| AF |
| AE |
（2）写出与
| AD |
考点：向量的模,相等向量与相反向量
专题：平面向量及应用
分析：（1）根据相等向量的定义：方向相同，长度相等的向量是相等向量解答；
（2）只要长度相等的向量即为模相等的向量．
（2）只要长度相等的向量即为模相等的向量．
解答：
解：（1）与
相等的向量有
，
；与
相等的向量有
；
（2）与
模相等的向量
，
，
．
| AF |
| BE |
| CD |
| AE |
| BD |
（2）与
| AD |
| DA |
| CF |
| FC |
点评：本题考查了相等向量以及模相等的向量；向量要有两个条件确定：长度和方向．
练习册系列答案
相关题目
若x，y满足
且z=ax+2y仅在点（3，4）处取得最小值，则a的取值范围是（ ）
|
| A、[-4，+∞） |
| B、（-4，+∞） |
| C、（-∞，-4] |
| D、（-∞，-4） |
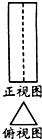某几何体的正视图和俯视图如图所示，若正视图是面积为3的矩形，俯视图是边长为1的正三角形，则该几何体的侧视图的面积为（ ）| A、3 | ||||
B、3
| ||||
C、
| ||||
| D、9 |