题目内容
袋中有大小、质地相同的红、黑球各一个,现有放回地随机摸取3次,每次摸取一个球若摸出红球,得2分,摸出黑球,得1分,则3次摸球所得总分至少是4分的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:一共有8种不同的结果,“3次摸球所得总分为低于4分”为事件A,事件A包含的基本事件为:(黑、黑、黑),由此利用对立事件概率计算公式能求出3次摸球所得总分至少是4分的概率.
解答:
解:一共有8种不同的结果,列举如下:
(红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、(黑、黑、红)、(黑、黑、黑)
“3次摸球所得总分为低于4分”为事件A
事件A包含的基本事件为:(黑、黑、黑),
∴3次摸球所得总分至少是4分的概率:
p=1-p(A)=1-
=
.
故答案为:
.
(红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、(黑、黑、红)、(黑、黑、黑)
“3次摸球所得总分为低于4分”为事件A
事件A包含的基本事件为:(黑、黑、黑),
∴3次摸球所得总分至少是4分的概率:
p=1-p(A)=1-
| 1 |
| 8 |
| 7 |
| 8 |
故答案为:
| 7 |
| 8 |
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意对数事件概率计算公式的合理运用.

练习册系列答案
相关题目
设实数列{an}和{bn}分别为等差数列与等比数列,且a1=b1=8,a4=b4=1,则以下结论正确的是( )
| A、a2>b2 |
| B、a3<b3 |
| C、a5>b5 |
| D、a6>b6 |
已知全集U={1,2,3,4,5},A={1,2,4},B={2,5},则(∁UA)∪B=( )
| A、{3,4,5} |
| B、{2,3,5} |
| C、{5} |
| D、{3} |
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )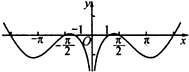

A、f(x)=
| ||
| B、f(x)=(lnx)cos2x | ||
| C、f(x)=(ln|x|)sin2x | ||
| D、f(x)=(ln|x|)cosx |