题目内容
12.如图在直角梯形ABCP中,AP∥BC,AB=BC=$\frac{1}{2}$AP=2,D是AP的中点,E,G分别为PC,CB的中点,将△PCD沿CD折起,使得PD⊥平面ABCD,F为线段PD上一动点.当二面角G-EF-D的大小为$\frac{π}{4}$时,求FG与平面PBC所成角的余弦值.
分析 由题意可知,AD⊥DC,AD⊥PD,DC⊥PD,以D为原点,分别以DA,DC,DP所在直线为x,y,z轴距离空间直角坐标系,利用空间向量结合二面角G-EF-D的大小为$\frac{π}{4}$,求出F得位置可得F的坐标,进一步求出FG与平面PBC所成角的余弦值.
解答 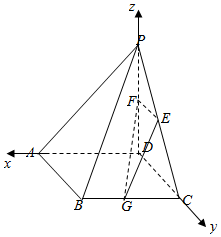 解:由题意可知,AD⊥DC,AD⊥PD,DC⊥PD,以D为原点,
解:由题意可知,AD⊥DC,AD⊥PD,DC⊥PD,以D为原点,
分别以DA,DC,DP所在直线为x,y,z轴距离空间直角坐标系,
∵AB=BC=$\frac{1}{2}$AP=2,且E,G分别为PC,CB的中点,
∴G(1,2,0),C(0,2,0),P(0,0,2),E(0,1,1),设F(0,0,a),
∴$\overrightarrow{GF}$=(-1,-2,a),$\overrightarrow{GE}$=(-1,-1,1),
设平面EFG的一个法向量为$\overrightarrow{n}$=(x,y,z),
则有$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{GE}=-x-y+z=0}\\{\overrightarrow{n}•\overrightarrow{GF}=-x-2y+az=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=(2-a,a-1,1).
又平面EFD的一个法向量$\overrightarrow{m}$=(1,0,0),
∴|cos<$\overrightarrow{n},\overrightarrow{m}$>|=$\frac{|2-a|}{\sqrt{(2-a)^{2}+(a-1)^{2}+1}×1}$=$\frac{\sqrt{2}}{2}$,
解得a=1,∴$\overrightarrow{GF}$=(-1,-2,1),
设平面PBC的法向量$\overrightarrow{r}$=(x,y,z),
∵$\overrightarrow{PC}$=(0,2,-2),$\overrightarrow{BC}$=(-2,0,0),
则有$\left\{\begin{array}{l}{\overrightarrow{r}•\overrightarrow{PC}=2y-2z=0}\\{\overrightarrow{r}•\overrightarrow{BC}=-2x=0}\end{array}\right.$,取z=1,得$\overrightarrow{r}$=(0,1,1).
设FG与平面PBC所成角为θ,
则有sinθ=|cos<$\overrightarrow{GF},\overrightarrow{r}$>|=$\frac{|\overrightarrow{FG}•\overrightarrow{r}|}{|\overrightarrow{FG}|•|\overrightarrow{r}|}$=$\frac{1}{\sqrt{6}•\sqrt{2}}=\frac{\sqrt{3}}{6}$,
∴cosθ=$\sqrt{1-si{n}^{2}θ}=\frac{\sqrt{33}}{6}$.
∴FG与平面PBC所成角的余弦值为$\frac{{\sqrt{33}}}{6}$.
点评 本题考查直线与平面所成角的余弦值的求法,注意向量法的合理运用,是中档题.

| A. | -$\frac{21}{2}$ | B. | -$\frac{5}{4}$ | C. | -1 | D. | -$\frac{15}{8}$ |
| 日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
| 温差x°C | 12 | 11 | 13 | 10 | 8 |
| 发芽率y颗 | 26 | 25 | 30 | 23 | 16 |
(2)请根据4月1日、4月2日、4月3日这3天的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)根据(2)中所得的线性回归方程,预测温差为16°C时,种子发芽的颗数.
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
| A. | 0≤a≤2 | B. | 0≤a | C. | 2≤a | D. | a≤2 |