题目内容
8.设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R.(1)求f(x)的单调区间;
(2)若f(x)存在极值点x0,且f(x1)=f(x0),其中x1≠x0,求证:x1+2x0=3;
(3)设$\frac{3}{4}≤a<3$,函数g(x)=|f(x)|,求证:g(x)在区间[0,2]上的最大值不小于$\frac{1}{4}$.
分析 (1)求出函数的导数,通过讨论a的范围求出函数的单调区间即可;
(2)求出${({x_0}-1)^2}=\frac{a}{3}$,得到f(x0)的解析式,求出f(3-2x0)=f(x0)=f(x1),从而证出结论即可;
(3)求出f(x)在区间[0,2]上的取值范围,求出M的最大值,从而证出结论即可.
解答 (1)解:由f(x)=(x-1)3-ax-b,可得f'(x)=3(x-1)2-a.
下面分两种情况讨论:
①当a≤0时,有f'(x)=3(x-1)2-a≥0恒成立,所以f(x)的单调递增区间为(-∞,+∞);
②当a>0时,令f'(x)=0,解得$x=1+\frac{{\sqrt{3a}}}{3}$,或$x=1-\frac{{\sqrt{3a}}}{3}$.
当x变化时,f'(x),f(x)的变化情况如下表:
| x | $(-∞,1-\frac{{\sqrt{3a}}}{3})$ | $1-\frac{{\sqrt{3a}}}{3}$ | $(1-\frac{{\sqrt{3a}}}{3},1+\frac{{\sqrt{3a}}}{3})$ | $1+\frac{{\sqrt{3a}}}{3}$ | $(1+\frac{{\sqrt{3a}}}{3},+∞)$ |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 极大值 | 极小值 |
(2)证明:因为f(x)存在极值点,所以由(1)知a>0,且x0≠1,
由题意,得$f'({x_0})=3{({x_0}-1)^2}-a=0$,即${({x_0}-1)^2}=\frac{a}{3}$,
进而$f({x_0})=-\frac{2a}{3}{x_0}-\frac{a}{3}-b$,
又$f(3-2{x_0})={(2-2{x_0})^3}-3(3-2{x_0}){({x_0}-1)^2}-b$=${({x_0}-1)^2}(8-8{x_0}-9+6{x_0})-b$=${({x_0}-1)^2}(-2{x_0}-1)-b$,
即为f(3-2x0)=f(x0)=f(x1),即有3-2x0=x1,即为x1+2x0=3.
(3)证明:设g(x)在区间[0,2]上的最大值为M,max{x,y}表示x,y两数的最大值;
当$\frac{3}{4}≤a<3$时,$1-\frac{{2\sqrt{3a}}}{3}≤0<1-\frac{{\sqrt{3a}}}{3}1+\frac{{\sqrt{3a}}}{3}<2≤1+\frac{{2\sqrt{3a}}}{3}$,
由(1)(2)知,$f(0)≥f(1-\frac{{2\sqrt{3a}}}{3})=f(1+\frac{{\sqrt{3a}}}{3})$,$f(2)≤f(1+\frac{{2\sqrt{3a}}}{3})=f(1-\frac{{\sqrt{3a}}}{3})$,
所以f(x)在区间[0,2]上的取值范围为$[{f(1+\frac{{\sqrt{3a}}}{3}),f(1-\frac{{\sqrt{3a}}}{3})}]$,
因此$M=max\left\{{|f(1+\frac{{\sqrt{3a}}}{3})|,|f(1-\frac{{\sqrt{3a}}}{3})|}\right\}$
=$max\left\{{|1-\frac{2a}{9}\sqrt{3a}-a-b|,|\frac{2a}{9}\sqrt{3a}-a-b|}\right\}$
=$max\left\{{|1-\frac{2a}{9}\sqrt{3a}-(a+b)|,|\frac{2a}{9}\sqrt{3a}-(a+b)|}\right\}$
=$\frac{2a}{9}\sqrt{3a}+|a+b|≥\frac{2}{9}×\frac{3}{4}×\sqrt{3×\frac{3}{4}}=\frac{1}{4}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.

练习册系列答案
相关题目
18.用平行于圆锥底面的截面去截圆锥,所得小圆锥的侧面积与原来大圆锥的侧面积的比是$\frac{1}{2}$,则小圆锥的高与大圆锥的高的比是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
19.设a,b,c是△ABC三个内角A,B,C所对应的边,且lgsinA,lgsinB,lgsinC成等差数列,那么直线xsinC-ysinA-a=0与直线xsin2B+ysin2C-c=0的位置关系( )
| A. | 平行 | B. | 垂直 | C. | 相交但不垂直 | D. | 重合 |
16.设U=R,A={x|log2x>1},B={x|2x>1},则B∩∁UA=( )
| A. | {x|x>0} | B. | {x|x>2} | C. | {x|0<x≤2} | D. | {x|0≤x<1} |
3.已知a,b,c是锐角△ABC中的角A、B、C的对边,若$B=\frac{π}{4}$,则$\frac{acosC-ccosA}{b}$的取值范围为( )
| A. | (-1,1) | B. | $(-\frac{1}{2},\frac{1}{2})$ | C. | $(-\sqrt{2},\sqrt{2})$ | D. | $(-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2})$ |
13.某四棱锥的三视图如图所示,则该四棱锥的外接球的表面积是( )
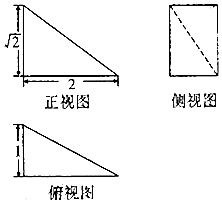

| A. | 4π | B. | 6π | C. | 7π | D. | 12π |
17.已知两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,则下列结论不正确的是( )
| A. | $\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为cosθ | B. | $\overrightarrow{{e}_{1}^{2}}$=$\overrightarrow{{e}_{2}^{2}}$ | ||
| C. | ($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$) | D. | |$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$|=1 |
18.要得到函数f(x)=sin2x,x∈R,只需将函数g(x)=cos2x,x∈R的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |