题目内容
12.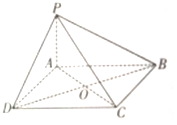 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.(Ⅰ)求证:平面PAC⊥平面PBD;
(Ⅱ)直线PD与过直线AC的平面α平行,平面α与棱PB交于点M,指明点M的位置,并证明.
分析 (I)根据线面垂直的判断定理可得PA⊥底面ABCD,即可得到PA⊥BD,得到BD⊥AC,故BD⊥平面PAC,于是平面PBD⊥平面PAC;
(Ⅱ)点M是棱PB的中点,根据线面平行的性质,即可求出PD∥OM,即可得到M为PB的中点.
解答 证明(Ⅰ):∵PA⊥AB,PA⊥AD,
∴PA⊥面ABCD
∴PA⊥BD
又已知ABCD为平行四边形,且AB=AD,
∴四边形ABCD为菱形,
∴BD⊥AC,
∴BD⊥平面PAC
又BD?平面PBD,∴平面PBD⊥平面PAC;
(Ⅱ)点M是棱PB的中点,
证明:如图,
连接MA,MC,MO,
∵PD∥平面MAC,平面PDB∩平面MAC=OM,PD?平面PDB
∴PD∥OM
又∵点O为BD的中点,
∴点M为PB的中点.
点评 本题考查了面面垂直的判定以及线面平行的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知a,b,c是锐角△ABC中的角A、B、C的对边,若$B=\frac{π}{4}$,则$\frac{acosC-ccosA}{b}$的取值范围为( )
| A. | (-1,1) | B. | $(-\frac{1}{2},\frac{1}{2})$ | C. | $(-\sqrt{2},\sqrt{2})$ | D. | $(-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2})$ |
17.已知两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,则下列结论不正确的是( )
| A. | $\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为cosθ | B. | $\overrightarrow{{e}_{1}^{2}}$=$\overrightarrow{{e}_{2}^{2}}$ | ||
| C. | ($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$) | D. | |$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$|=1 |
4.执行如图所示的程序框图,若$a=\frac{9}{4}$,则输出S的值为( )
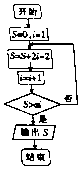

| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
1.曲线M的方程为$\sqrt{{{(x-1)}^2}+{y^2}}+\sqrt{{{(x+1)}^2}+{y^2}}$=4,直线y=k(x+1)交曲线M于A,B两点,点C(1,0),则△ABC的周长为( )
| A. | 4 | B. | $4\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 8 |