题目内容
2.已知函数f(x)=axsinx-$\frac{3}{2}({a∈R})$,且在$[{0,\frac{π}{2}}]$上的最大值为$\frac{π-3}{2}$,则实数a的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 由题意,可借助导数研究函数f(x)在[0,$\frac{π}{2}$]上的单调性,确定出最值,令最值等于$\frac{π-3}{2}$,即可得到关于a的方程,由于a的符号对函数的最值有影响,故可以对a的取值范围进行讨论,分类求解.
解答 解:由已知得f′(x)=a(sinx+xcosx),
对于任意的x∈[0,$\frac{π}{2}$],有sinx+xcosx>0,当a=0时,f(x)=-$\frac{3}{2}$,不合题意;
当a<0时,x∈[0,$\frac{π}{2}$],f′(x)<0,从而f(x)在[0,$\frac{π}{2}$]单调递减,
又函数在上图象是连续不断的,故函数f(x)在[0,$\frac{π}{2}$]上的最大值为f(0)=-$\frac{3}{2}$,不合题意;
当a>0时,x∈[0,$\frac{π}{2}$],f′(x)>0,从而f(x)在[0,$\frac{π}{2}$]单调递增,
又函数在上图象是连续不断的,故函数f(x)在[0,$\frac{π}{2}$]上的最大值为f($\frac{π}{2}$)=$\frac{π}{2}$a-$\frac{3}{2}$=$\frac{π-3}{2}$,解得a=1,
故选:B
点评 本题考察了利用导函数研究其单调性和函数的最值问题,需要分类讨论.属于中档题

练习册系列答案
相关题目
12.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
由表中数据,求得线性回归方程为y=-20x+a,则a的值为250.
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
13.某四棱锥的三视图如图所示,则该四棱锥的外接球的表面积是( )
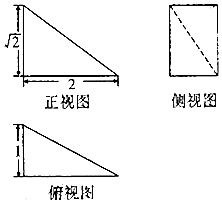

| A. | 4π | B. | 6π | C. | 7π | D. | 12π |
17.已知两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,则下列结论不正确的是( )
| A. | $\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为cosθ | B. | $\overrightarrow{{e}_{1}^{2}}$=$\overrightarrow{{e}_{2}^{2}}$ | ||
| C. | ($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$) | D. | |$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$|=1 |
7.在等比数列{an}中,a1=3,公比$q=\sqrt{2}$,则a7等于( )
| A. | 12 | B. | 15 | C. | 18 | D. | 24 |
14.与椭圆$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{24}$=1有公共焦点,且离心率e=$\frac{5}{3}$的双曲线方程是( )
| A. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1 |