题目内容
9.从甲、乙、丙等5名候选学生中选出2名作为校运动会志愿者,则甲、乙、丙中有2人被选中的概率是( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
分析 先求出基本事件总数$n={C}_{5}^{2}=10$,再求出甲、乙、丙中有2人被选中包含的基本事件个数m=${C}_{3}^{2}$=3,由此能求出甲、乙、丙中有2人被选中的概率.
解答 解:从甲、乙、丙等5名候选学生中选出2名作为校运动会志愿者,
基本事件总数$n={C}_{5}^{2}=10$,
甲、乙、丙中有2人被选中包含的基本事件个数m=${C}_{3}^{2}$=3,
∴甲、乙、丙中有2人被选中的概率是p=$\frac{m}{n}$=$\frac{3}{10}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
19.设a,b,c是△ABC三个内角A,B,C所对应的边,且lgsinA,lgsinB,lgsinC成等差数列,那么直线xsinC-ysinA-a=0与直线xsin2B+ysin2C-c=0的位置关系( )
| A. | 平行 | B. | 垂直 | C. | 相交但不垂直 | D. | 重合 |
17.已知两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,则下列结论不正确的是( )
| A. | $\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为cosθ | B. | $\overrightarrow{{e}_{1}^{2}}$=$\overrightarrow{{e}_{2}^{2}}$ | ||
| C. | ($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$) | D. | |$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$|=1 |
4.执行如图所示的程序框图,若$a=\frac{9}{4}$,则输出S的值为( )
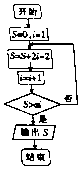

| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
14.与椭圆$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{24}$=1有公共焦点,且离心率e=$\frac{5}{3}$的双曲线方程是( )
| A. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1 |
1.曲线M的方程为$\sqrt{{{(x-1)}^2}+{y^2}}+\sqrt{{{(x+1)}^2}+{y^2}}$=4,直线y=k(x+1)交曲线M于A,B两点,点C(1,0),则△ABC的周长为( )
| A. | 4 | B. | $4\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 8 |
18.要得到函数f(x)=sin2x,x∈R,只需将函数g(x)=cos2x,x∈R的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
19.若方程mx2+(3-m)y2=1表示双曲线,则实数m的取值范围是( )
| A. | m<0 | B. | m>3 | C. | 0<m<3 | D. | m<0或m>3 |