题目内容
命题：“存在x0∈R，使得x02＜0”的否定为（ ）
| A、对任意的x∈R都有x2＜0 |
| B、存在x0∈R使得x02＞0 |
| C、存在x0∈R使得x02≥0 |
| D、对任意的x∈R都有x2≥0 |
考点：特称命题,命题的否定
专题：操作型,简易逻辑
分析：利用特称命题的否定是全称命题写出结果即可．
解答：
解：∵特称命题的否定是全称命题．
∴命题：“存在x0∈R，使得x02＜0”否定是：“对任意的x∈R都有x2≥0”．
故选：D．
∴命题：“存在x0∈R，使得x02＜0”否定是：“对任意的x∈R都有x2≥0”．
故选：D．
点评：这类问题的常见错误是没有把全称量词改为存在量词，或者对于“＞”的否定用“＜”了．这里就有注意量词的否定形式．如“都是”的否定是“不都是”，而不是“都不是”．特称命题的否定是全称命题，“存在”对应“任意”．
练习册系列答案
相关题目
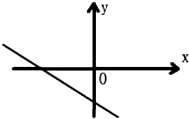
已知一次函数y=kx+b的图象如图所示，则k，b的符号是（ ）
| A、k＞0，b＞0 |
| B、k＞0，b＜0 |
| C、k＜0，b＞0 |
| D、k＜0，b＜0 |
已知i为虚数单位，若复数（a2-1）+（a-1）i（a∈R）是纯虚数，则实数a的值为（ ）
| A、±1 | B、-1 | C、0 | D、1 |
已知过点A（-2，m）和B（m，4）的直线l1与直线l2：2x+y-1=0垂直，则m的值为（ ）
| A、-8 | B、0 | C、2 | D、10 |