题目内容
已知F1,F2是椭圆
+y2=1的左右焦点,过F1作倾斜角为45°的直线与椭圆相交于A,B两点.
(1)求△F2AB的周长
(2)求AB的长
(3)求△F2AB的面积.
| x2 |
| 2 |
(1)求△F2AB的周长
(2)求AB的长
(3)求△F2AB的面积.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)由
+y2=1 可得 a=
,△F2AB的周长=4a=4
.
(2)把 y=x+1 代入 x2+2y2=2 求得交点A,B的坐标,再利用两点之间的距离公式即可得出|AB|=
.
(3)利用点到直线的距离公式可得点F2到直线AB的距离d,即可得出S=
•|AB|•d.
| x2 |
| 2 |
| 2 |
| 2 |
(2)把 y=x+1 代入 x2+2y2=2 求得交点A,B的坐标,再利用两点之间的距离公式即可得出|AB|=
| (x1-x2)2+(y1-y2)2 |
(3)利用点到直线的距离公式可得点F2到直线AB的距离d,即可得出S=
| 1 |
| 2 |
解答:
解:(1)由
+y2=1 可得 a=
,b=1=c,
∴△F2AB的周长=4a=4
.
(2)把 y=x+1 代入 x2+2y2=2 得3x2+4x=0,
解得x1=0 x2=-
,y1=1,y2=-
,
∴|AB|=
=
.
(3)点F2到直线AB的距离d=
=
,
S=
•|AB|•d=
•
=
.
| x2 |
| 2 |
| 2 |
∴△F2AB的周长=4a=4
| 2 |
(2)把 y=x+1 代入 x2+2y2=2 得3x2+4x=0,
解得x1=0 x2=-
| 4 |
| 3 |
| 1 |
| 3 |
∴|AB|=
| (x1-x2)2+(y1-y2)2 |
4
| ||
| 3 |
(3)点F2到直线AB的距离d=
| |1-0+1| | ||
|
| 2 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
| 2 |
| 4 |
| 3 |
点评:本题考查了直线与椭圆相交问题、椭圆的标准方程及其性质、两点之间的距离公式、三角形的面积计算公式,
考查了计算能力,属于基础题.
考查了计算能力,属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
在等比数列{an}中,a1=1,公比|q|≠1.若am=a1a2a3a4a5,则m=( )
| A、9 | B、10 | C、11 | D、12 |
集合A={x|
≥0}B={x||x-1|<3},则A∩B=( )
| x-1 |
| x+1 |
| A、(-2,-1) |
| B、[1,4) |
| C、(-2,-1)∪[1,4) |
| D、(-2,4) |
函数f(x)=
,若函数g(x)=f(x)-kx+k的零点有2个,则k的取值范围( )
|
| A、(1,2] |
| B、(0,1] |
| C、(1,3] |
| D、(1,+∞) |
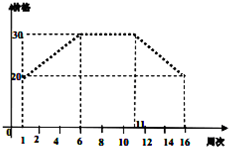 在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.
在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.