题目内容
直线x=ky+3与双曲线
-
=1只有一个公共点，则k的值有（ ）
| x2 |
| 9 |
| y2 |
| 4 |
| A、1个 | B、2个 |
| C、3个 | D、无数多个 |
考点：直线与圆锥曲线的综合问题
专题：计算题,分类讨论,圆锥曲线的定义、性质与方程
分析：将直线x=ky+3代入双曲线
-
=1，可化为（4k2-9）y2+24ky=0．分类讨论：当4k2-9=0时，可得k=±
，此时直线与双曲线的渐近线平行，满足题意；当4k2-9≠0时，由直线与双曲线有且只有一个公共点，可得△=0，解出即可．
| x2 |
| 9 |
| y2 |
| 4 |
| 3 |
| 2 |
解答：
解：x=ky+3代入双曲线
-
=1，可化为（4k2-9）y2+24ky=0．
①当4k2-9=0时，可得k=±
，此时直线与双曲线的渐近线平行，直线与双曲线有且只有一个交点，满足题意；
②当4k2-9≠0时，由直线与双曲线有且只有一个公共点，可得△=（24k）2-0=0，解得k=0．此时满足条件．
综上可得：k=±
，0．
故选：C．
| x2 |
| 9 |
| y2 |
| 4 |
①当4k2-9=0时，可得k=±
| 3 |
| 2 |
②当4k2-9≠0时，由直线与双曲线有且只有一个公共点，可得△=（24k）2-0=0，解得k=0．此时满足条件．
综上可得：k=±
| 3 |
| 2 |
故选：C．
点评：本题考查了直线与双曲线的位置关系及其性质、一元二次方程与△的关系、分类讨论等基础知识与基本方法，属于难题．
练习册系列答案
相关题目
给出下列命题：
①若a，b∈R+，a≠b，则a3+b3＞a2b+ab2；
②若a，b，c∈R，则a2+b2+c2≥ab+bc+ca；
③若a＞0，b＞0，a+b=2，则
+
≤
；
④若
，则
；
⑤函数y=
的最小值等于2．
其中正确命题的个数为（ ）
①若a，b∈R+，a≠b，则a3+b3＞a2b+ab2；
②若a，b，c∈R，则a2+b2+c2≥ab+bc+ca；
③若a＞0，b＞0，a+b=2，则
| a |
| b |
| 2 |
④若
|
|
⑤函数y=
| x2+2014 | ||
|
其中正确命题的个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
下列判断错误的是（ ）
| A、命题“?x∈R，2x＞0”的否定是“?x0∈R，2x0≤0” | ||||
| B、命题“若xy=0，则x=0”的否命题为“若xy≠0，则x≠0” | ||||
| C、函数y=2x-3+1的图象恒过定点A（3，2） | ||||
D、“sinα=
|
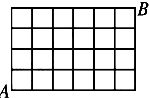某市有7条南北向街道，5条东西向街道．图中共有m个矩形，从A点走到B点最短路线的走法有n种，则m，n的值分别为（ ）| A、m=90，n=210 |
| B、m=210，n=210 |
| C、m=210，n=792 |
| D、m=90，n=792 |
下列命题中的真命题是（ ）
| A、若a＞b＞0，a＞c，则a2＞bc | ||||
B、若a＞b＞c，则
| ||||
| C、若a＞b，n∈N*，则an＞bn | ||||
| D、若a＞b＞0，则1na＜1nb |
若直线x-y+2=0与圆C：（x-3）2+（y-3）2=4相交于A、B两点，则
•
的值为（ ）
| CA |
| CB |
| A、-1 | B、0 | C、1 | D、6 |
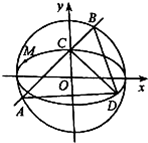已知椭圆C1：