题目内容
有下列四个命题:
①“若A∪B=B,则A?B”;
②“若b≤1,则方程x2-2bx+b2+b=0有实根”的逆否命题;
③“若y=f(x)是奇函数,则f(0)=0”的否命题;
④“若x>y>1,则logx3<logy3”的逆命题.
其中真命题的个数是( )
①“若A∪B=B,则A?B”;
②“若b≤1,则方程x2-2bx+b2+b=0有实根”的逆否命题;
③“若y=f(x)是奇函数,则f(0)=0”的否命题;
④“若x>y>1,则logx3<logy3”的逆命题.
其中真命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:根据集合包含关系和并集的含义,可举出反例说明①为假命题;
运用一元二次方程根的判别式,结合不等式的基本性质,可得②为真命题;
依据函数的奇偶性,可举出反例得到③为假命题;
由换底公式以及logx3<logy3,即可得到④为假命题.
运用一元二次方程根的判别式,结合不等式的基本性质,可得②为真命题;
依据函数的奇偶性,可举出反例得到③为假命题;
由换底公式以及logx3<logy3,即可得到④为假命题.
解答:
解:①举反例:A={1,2},B={1,2,3}
此时A?B,但A∪B={1,2,3}=B,故①是假命题;
②对于③,“若b≤1,则方程x2-2bx+b2+b=0有实根”逆否命题是:
若x2-2bx+b2+b=0没有实数根,则b>1.
若x2-2bx+b2+b=0没有实数根,可得△=-4b<0⇒b>0⇒b>-1,
可知当x2-2bx+b2+b=0没有实数根时,b>-1成立,故②是假命题;
③“若y=f(x)是奇函数,则f(0)=0”的否命题是:
若y=f(x)不是奇函数,则f(0)≠0,
若f(x)=x2,满足y=f(x)不是奇函数,但f(0)=0,故③是假命题;
④“若x>y>1,则logx3<logy3”的逆命题是:.
“若logx3<logy3,则x>y>1”,
由于logx3<logy3,则
<
,显然当0<x<1,y>1时满足
<
,故④是假命题.
故这4 个命题中真命题的个数是0,
故选:A
此时A?B,但A∪B={1,2,3}=B,故①是假命题;
②对于③,“若b≤1,则方程x2-2bx+b2+b=0有实根”逆否命题是:
若x2-2bx+b2+b=0没有实数根,则b>1.
若x2-2bx+b2+b=0没有实数根,可得△=-4b<0⇒b>0⇒b>-1,
可知当x2-2bx+b2+b=0没有实数根时,b>-1成立,故②是假命题;
③“若y=f(x)是奇函数,则f(0)=0”的否命题是:
若y=f(x)不是奇函数,则f(0)≠0,
若f(x)=x2,满足y=f(x)不是奇函数,但f(0)=0,故③是假命题;
④“若x>y>1,则logx3<logy3”的逆命题是:.
“若logx3<logy3,则x>y>1”,
由于logx3<logy3,则
| lg3 |
| lgx |
| lg3 |
| lgy |
| lg3 |
| lgx |
| lg3 |
| lgy |
故这4 个命题中真命题的个数是0,
故选:A
点评:本题主要考查四种命题的关系,以及四种命题的真假关系,互为逆否命题的两个命题为等价问题.

练习册系列答案
相关题目
给出下列命题:
①若a,b∈R+,a≠b,则a3+b3>a2b+ab2;
②若a,b,c∈R,则a2+b2+c2≥ab+bc+ca;
③若a>0,b>0,a+b=2,则
+
≤
;
④若
,则
;
⑤函数y=
的最小值等于2.
其中正确命题的个数为( )
①若a,b∈R+,a≠b,则a3+b3>a2b+ab2;
②若a,b,c∈R,则a2+b2+c2≥ab+bc+ca;
③若a>0,b>0,a+b=2,则
| a |
| b |
| 2 |
④若
|
|
⑤函数y=
| x2+2014 | ||
|
其中正确命题的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
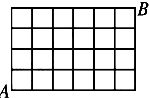 某市有7条南北向街道,5条东西向街道.图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )
某市有7条南北向街道,5条东西向街道.图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )| A、m=90,n=210 |
| B、m=210,n=210 |
| C、m=210,n=792 |
| D、m=90,n=792 |
下列命题中的真命题是( )
| A、若a>b>0,a>c,则a2>bc | ||||
B、若a>b>c,则
| ||||
| C、若a>b,n∈N*,则an>bn | ||||
| D、若a>b>0,则1na<1nb |
下列有关命题说法正确的是( )
A、命题p:“存在x∈R,sinx+cosx=
| ||
| B、“a=1”是“函数f(x)=cos2ax-sin2ax的周期T=π”的充分必要条件 | ||
| C、命题“存在x∈R,使得x2+x+1=0”的否定是:“对任意x∈R,x2+x+1≥0” | ||
D、命题“若tanα≠1,则α≠
|
若直线x-y+2=0与圆C:(x-3)2+(y-3)2=4相交于A、B两点,则
•
的值为( )
| CA |
| CB |
| A、-1 | B、0 | C、1 | D、6 |