题目内容
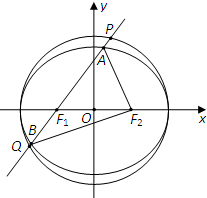 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 2 |
点A在轴上方).当α=
| π |
| 4 |
| 14 |
(1)求圆O和椭圆C的方程;
(2)若点M是椭圆C上一点,求当AF2,BF2,AB成等差数列时,△MPQ面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)取PQ的中点D,连接OD,OP,求出OD,利用弦PQ的长为
,求出OQ,可得a,b,即可求圆O和椭圆C的方程;
(2)设|AF2|=s,|BF2|=t,利用AF2,BF2,AB成等差数列,求出t,设B(x0,y0),则由
,得B的坐标,可得PQ的方程,求出PQ,椭圆C上一点到直线PQ的距离的最大值,即可求△MPQ面积的最大值.
| 14 |
(2)设|AF2|=s,|BF2|=t,利用AF2,BF2,AB成等差数列,求出t,设B(x0,y0),则由
|
解答:
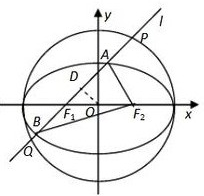 解:(1)取PQ的中点D,连接OD,OP,
解:(1)取PQ的中点D,连接OD,OP,
由α=
,c=1,可得OD=
,
∵弦PQ的长为
,
∴OQ2=
+OD2=4,
∴a2=4,b2=3,
∴圆O的方程为x2+y2=4,椭圆C的方程为
+
=1;
(2)设|AF2|=s,|BF2|=t,则
|AF1|+|AF2|=2a=4,|BF1|+|BF2|=2a=4,
∵AF2,BF2,AB成等差数列,
∴2t=s+8-s-t,
∴t=
,
设B(x0,y0),则由
,得B(-
,-
),
∴k=
,
∴PQ:y=
(x+1)
∴O到PQ的距离为d=
,
∴PQ=2
=
,
又∵椭圆C上一点到直线PQ的距离的最大值为
,
∴△MPQ面积的最大值
•
•
=
.
 解:(1)取PQ的中点D,连接OD,OP,
解:(1)取PQ的中点D,连接OD,OP,由α=
| π |
| 4 |
| ||
| 2 |
∵弦PQ的长为
| 14 |
∴OQ2=
| PQ2 |
| 4 |
∴a2=4,b2=3,
∴圆O的方程为x2+y2=4,椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设|AF2|=s,|BF2|=t,则
|AF1|+|AF2|=2a=4,|BF1|+|BF2|=2a=4,
∵AF2,BF2,AB成等差数列,
∴2t=s+8-s-t,
∴t=
| 8 |
| 3 |
设B(x0,y0),则由
|
| 4 |
| 3 |
| ||
| 3 |
∴k=
| 15 |
∴PQ:y=
| 15 |
∴O到PQ的距离为d=
| ||
| 4 |
∴PQ=2
4-
|
| 7 |
| 2 |
又∵椭圆C上一点到直线PQ的距离的最大值为
3
| ||||
| 4 |
∴△MPQ面积的最大值
| 1 |
| 2 |
| 7 |
| 2 |
3
| ||||
| 4 |
21
| ||||
| 16 |
点评:本题考查圆和椭圆的方程,考查三角形面积的计算,考查等差数列的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列命题中的真命题是( )
| A、若a>b>0,a>c,则a2>bc | ||||
B、若a>b>c,则
| ||||
| C、若a>b,n∈N*,则an>bn | ||||
| D、若a>b>0,则1na<1nb |
若直线x-y+2=0与圆C:(x-3)2+(y-3)2=4相交于A、B两点,则
•
的值为( )
| CA |
| CB |
| A、-1 | B、0 | C、1 | D、6 |
 已知椭圆C1:
已知椭圆C1: