题目内容

14．在区间[1，5]随机地取一个数m，则方程m2x2+4y2=1表示焦点在y轴上的椭圆的概率是（　　）
A．$\frac{3}{5}$B．$\frac{1}{5}$C．$\frac{1}{4}$D．$\frac{3}{4}$

分析 表示焦点在y轴上的椭圆，求出m的范围，可得区间长度，求出在区间[1，5]上随机取一个实数m的区间长度，即可得出结论．

解答 解：若方程m2x2+4y2=1表示焦点在y轴上的椭圆，
则m2＞4，解得：m＞2，
故满足条件的概率是p=$\frac{5-2}{5-1}$=$\frac{3}{4}$，
故选：D．

点评 本题考查几何概型概率的求法，是较基础题，解题时要认真审题，注意几何概型的测度选择．

练习册系列答案
相关题目
4．已知命题p：?x0∈R，lnx0≥x0-1．命题q：?θ∈R，sinθ+cosθ＜1，．则下列命题中为真命题的是（　　）
A．p∧qB．（￢p）∧qC．（￢p）∧（￢q）D．p∧（￢q）
5．已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的非负半轴，建立平面直角坐标系xOy，若将曲线C向左平移1个单位长度后就得到了曲线C1，再将曲线C1上每一点的横坐标伸长为原来的$\sqrt{3}$倍，纵坐标保持不变就得到了曲线C2，已知直线l：x-y-6=0．
（1）求曲线C1上的点到直线l的距离的最大值；
（2）过点M（-1，0）且与直线l平行的直线l1交C2于A，B两点，求点M到A，B两点的距离之积．
2．如图画的某几何体的三视图，网格纸上小正方形的边长为1，则该几何体的体积为（　　）
A．48-πB．96-πC．48-2πD．96-2π
9．已知函数f（x）=sin（ωx+2φ）-2sinφcos（ωx+φ）（ω＞0，φ∈R）在（π，$\frac{3π}{2}$）上单调递减，则ω的取值范围是（　　）
A．（0，2]B．（0，$\frac{1}{2}$]C．[$\frac{1}{2}$，1]D．[$\frac{1}{2}$，$\frac{5}{4}$]
19．函数$f（x）=\sqrt{x-2}$的定义域是（　　）
A．（-∞，2）B．（-∞，2]C．（2，+∞）D．[2，+∞）
6．若函数y=2sinωx（ω＞0）在[-$\frac{π}{3}$，$\frac{π}{4}$]上的最小值是-2，但最大值不是2，则ω的取值范围是（　　）
A．（0，2）B．[$\frac{3}{2}$，2）C．（0，$\frac{3}{2}$]D．[2，+∞）
3．数列{an}的各项均为正数，其前n项和为Sn，已知$\frac{n{a}_{n+1}}{{a}_{n}}$$-\frac{（n+1）{a}_{n}}{{a}_{n+1}}$=1，且a1=$\frac{π}{3}$，则tanSn的取值集合是（　　）
A．{0，$\sqrt{3}$}B．{0，$\sqrt{3}$，$\frac{\sqrt{3}}{3}$}C．{0，$\sqrt{3}$，-$\frac{\sqrt{3}}{3}$}D．{0，$\sqrt{3}$，-$\sqrt{3}$}
4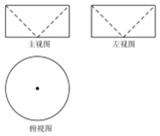．如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的体积为（　　）
A．$\frac{π}{2}$B．$\frac{π}{4}$C．$\frac{2π}{3}$D．$\frac{π}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网