题目内容

19．函数$f（x）=\sqrt{x-2}$的定义域是（　　）
A．（-∞，2）B．（-∞，2]C．（2，+∞）D．[2，+∞）

分析 根据函数f（x）的解析式，二次根式的被开方数大于或等于0，求出解集即可．

解答 解：函数f（x）=$\sqrt{x-2}$，
∴x-2≥0，
解得x≥2；
∴f（x）的定义域是[2，+∞）．
故选：D．

点评 本题考查了根据函数f（x）的解析式，求定义域的应用问题，是基础题．

练习册系列答案
相关题目
9．已知定义在R上的函数$f（x）=\frac{1}{2}（{sinωx+acosωx}）（{a∈R\;，\;\;0＜ω≤1}）$
满足：$f（x）=f（{\frac{π}{3}-x}）$，f（x-π）=f（x+π）．
（Ⅰ）求f（x）的解析式；
（Ⅱ）设不等的实数x1，${x_2}∈（{-\frac{π}{3}\;，\;\;\frac{5π}{3}}）$，且$f（{x_1}）=f（{x_2}）=-\frac{1}{2}$，求x1+x2的值．
10．若角α=-4，则α的终边在（　　）
A．第四象限B．第三象限C．第二象限D．第一象限
7．已知函数f（x）=x3+bx2+cx-1在x=-2时取得极值，且在点（-1，f（-1））处的切线的斜率为-3．
（1）求函数f（x）的解析式；
（2）求函数f（x）在区间[-1，2]上的最大值与最小值．
14．在区间[1，5]随机地取一个数m，则方程m2x2+4y2=1表示焦点在y轴上的椭圆的概率是（　　）
A．$\frac{3}{5}$B．$\frac{1}{5}$C．$\frac{1}{4}$D．$\frac{3}{4}$
4．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F，过点F作倾斜角为30°的直线与双曲线左右两支各有一个交点，过点F作倾斜角为60°的直线与双曲线右支交于不同的两点，则该双曲线离心率的取值范围是（　　）
A．（1，$\frac{2\sqrt{3}}{3}$）B．（$\frac{2\sqrt{3}}{3}$，2）C．[$\frac{2\sqrt{3}}{3}$，2]D．（2，+∞）
11．定义上凸函数如下：设f（x）为区间I上的函数，若对任意的x1，x2∈I总有f（$\frac{{x}_{1}+{x}_{2}}{2}$）≥$\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$，则称f（x）为I上的上凸函数，某同学查阅资料后发现了上凸函数的如下判定定理和性质定理：
判定定理：f（x）为上凸函数的充要条件是f″（x）≤0，x∈I，其中f″（x）为f（x）的导函数f′（x）的导数．
性质定理：若函数f（x）为区间I上的上凸函数，则对I内任意的x1，x2，…，xn，都有$\frac{f（{x}_{1}）+f（{x}_{2}）+…+f（{x}_{n}）}{n}$≤f（$\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$）．
请问：在△ABC中，sinA+sinB+sinC的最大值为$\frac{3\sqrt{3}}{2}$．
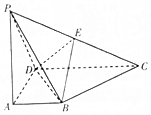8．如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，PA⊥BC，E是棱PC的中点，∠DAB=90°，AB∥CD，AD=CD=2AB=2．
（Ⅰ）求证：PA⊥平面ABCD；
（Ⅱ）若二面角E-BD-P大于60°，求四棱锥P-ABCD体积的取值范围．
9．设等差数列{an}的公差d＞0，前n项和为Sn，已知3$\sqrt{5}$是-a2与a9的等比中项，S10=-20．
（1）求数列{an}的通项公式；
（2）设bn=$\frac{1}{{a}_{n}|{a}_{n+1}|}$，求数列{bn}的前n项和Tn（n≥6）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网