题目内容
4．
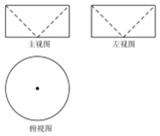如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的体积为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{π}{4}$ | C． | $\frac{2π}{3}$ | D． | $\frac{π}{3}$ |
分析 由题意，几何体是圆柱挖去圆锥所得，利用圆柱、圆锥的体积公式可得体积．
解答 解：由题意，几何体是圆柱挖去圆锥所得，体积为$π•{1}^{2}•1-\frac{1}{3}×π•{1}^{2}•1$=$\frac{2π}{3}$．
故选C．
点评 本题考查由三视图求体积，考查学生分析解决问题的能力，确定直观图的形状是关键．
练习册系列答案
阅读快车系列答案
相关题目
14．在区间[1，5]随机地取一个数m，则方程m2x2+4y2=1表示焦点在y轴上的椭圆的概率是（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
15．
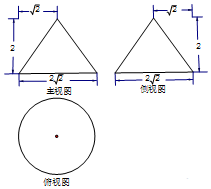某工件的三视图如图所示，现将该工件通过切割，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则新工件的体积为（ ）
某工件的三视图如图所示，现将该工件通过切割，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则新工件的体积为（ ）| A． | $\frac{1}{8}$ | B． | 1 | C． | 2 | D． | $\frac{4π}{3}$ |
如图，点C是以AB为直径的圆上一点，直角梯形BCDE所在平面与圆O所在平面垂直，且DE∥BC，DC⊥BC，DE=$\frac{1}{2}$BC=2，AC=CD=3．
13．从区间[-1，1]内随机取出一个数a，使3a+1＞0的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |
14．已知函数$f（x）={sin^4}x+{cos^4}x，x∈[-\frac{π}{4}，\frac{π}{4}]$，若f（x1）＜f（x2），则一定有（ ）
| A． | x1＜x2 | B． | x1＞x2 | C． | ${x_1}^2＜{x_2}^2$ | D． | ${x_1}^2＞{x_2}^2$ |