题目内容
5.已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的非负半轴,建立平面直角坐标系xOy,若将曲线C向左平移1个单位长度后就得到了曲线C1,再将曲线C1上每一点的横坐标伸长为原来的$\sqrt{3}$倍,纵坐标保持不变就得到了曲线C2,已知直线l:x-y-6=0.(1)求曲线C1上的点到直线l的距离的最大值;
(2)过点M(-1,0)且与直线l平行的直线l1交C2于A,B两点,求点M到A,B两点的距离之积.
分析 (1)化极坐标方程为 普通方程,利用点到直线的距离公式求出曲线C1上的点到直线l的距离的最大值;
(2)求出曲线C2的直角坐标方程,直线的参数方程,代入x2+3y2=3化简得:$2{t^2}-\sqrt{2}t-2=0$,利用参数的几何意义,求解点M到A,B两点的距离之积.
解答 解:(1)曲线C的直角坐标方程为(x-1)2+y2=1,
曲线C1的直角坐标方程为x2+y2=1,则曲线C1上的点到直线l的距离的最大值${d_{max}}=3\sqrt{2}+1$.---------(3分)
(2)设曲线C2上任意一点的坐标为(x′,y′),曲线C1上任意一点的坐标为(x,y),
由题意可得伸缩变换为$\left\{\begin{array}{l}{x^'}=\sqrt{3}x\\{y^'}=y\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{{\sqrt{3}}}{3}{x^'}\\ y={y^'}\end{array}\right.$,
代入曲线C1的直角坐标方程为x2+y2=1,可得曲线C2的直角坐标方程为$\frac{x^2}{3}+{y^2}=1$,
即x2+3y2=3,----------------(6分)
直线l1的参数方程为$\left\{\begin{array}{l}x=-1+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t.\end{array}\right.$(t为参数),
代入x2+3y2=3化简得:$2{t^2}-\sqrt{2}t-2=0$,得t1t2=-1,
∴|MA|•|MB|=|t1t2|=1----------------(10分)
点评 本题考查直线与椭圆的方程以及极坐标方程的应用,考查点到直线的距离公式的应用,考查计算能力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案| A. | $\frac{3+\sqrt{3}}{4}$a2 | B. | $\frac{3}{4}$a2 | C. | $\frac{3+\sqrt{3}}{2}$a2 | D. | $\frac{6+\sqrt{3}}{4}$a2 |
| A. | ?x∈(-∞,0),x3+x<0 | B. | ?x∈(-∞,0),x3+x≥0 | ||
| C. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}<0$ | D. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}≥0$ |
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{3}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
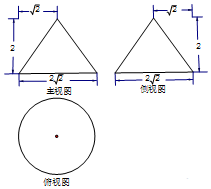 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )| A. | $\frac{1}{8}$ | B. | 1 | C. | 2 | D. | $\frac{4π}{3}$ |