题目内容
6.若函数y=2sinωx(ω>0)在[-$\frac{π}{3}$,$\frac{π}{4}$]上的最小值是-2,但最大值不是2,则ω的取值范围是( )| A. | (0,2) | B. | [$\frac{3}{2}$,2) | C. | (0,$\frac{3}{2}$] | D. | [2,+∞) |
分析 根据x∈[-$\frac{π}{3}$,$\frac{π}{4}$]求出ωx的取值范围,结合题意列出ω的不等式组,从而求出ω的取值范围.
解答 解:函数y=2sinωx(ω>0)在[-$\frac{π}{3}$,$\frac{π}{4}$]上的最小值是-2,但最大值不是2,
∴ωx的取值范围是[-$\frac{π}{3}$ω,$\frac{π}{4}$ω];
∴-$\frac{π}{3}$ω≤-$\frac{π}{2}$且$\frac{π}{4}$ω<$\frac{π}{2}$,
解得$\frac{3}{2}$≤ω<2,
∴ω的取值范围是[$\frac{3}{2}$,2).
故选:B.
点评 本题主要考查了正弦函数的最值应用问题,是基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
16.侧面都是直角三角形的正三棱锥,底面边长为a时,该三棱锥的全面积是( )
| A. | $\frac{3+\sqrt{3}}{4}$a2 | B. | $\frac{3}{4}$a2 | C. | $\frac{3+\sqrt{3}}{2}$a2 | D. | $\frac{6+\sqrt{3}}{4}$a2 |
17.已知sinθ>0且cosθ<0,则角θ的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.在区间[1,5]随机地取一个数m,则方程m2x2+4y2=1表示焦点在y轴上的椭圆的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
1.已知i是虚数单位,则$\frac{(-1+i)(1+i)}{{i}^{3}}$=( )
| A. | -2i | B. | 2i | C. | -i | D. | i |
18.设点P(x,y)在△ABC的内部及其边界上运动,其中A(1,1),B(2,4),C(3,1),则$\frac{y}{x}$的取值范围是( )
| A. | [$\frac{1}{3}$,+∞) | B. | [2,+∞) | C. | ($\frac{1}{3}$,2) | D. | [$\frac{1}{3}$,2] |
15.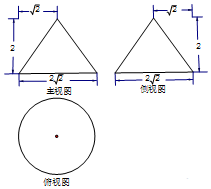 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )
 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为( )| A. | $\frac{1}{8}$ | B. | 1 | C. | 2 | D. | $\frac{4π}{3}$ |