题目内容
9.已知函数f(x)=sin(ωx+2φ)-2sinφcos(ωx+φ)(ω>0,φ∈R)在(π,$\frac{3π}{2}$)上单调递减,则ω的取值范围是( )| A. | (0,2] | B. | (0,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,1] | D. | [$\frac{1}{2}$,$\frac{5}{4}$] |
分析 利用积化和差公式化简2sinφcos(ωx+φ)=sin(ωx+2φ)-sinωx.可将函数化为y=Asin(ωx+φ)的形式,在(π,$\frac{3π}{2}$)上单调递减,结合三角函数的图象和性质,建立关系可求ω的取值范围.
解答 解:函数f(x)=sin(ωx+2φ)-2sinφcos(ωx+φ)(ω>0,φ∈R).
化简可得:f(x)=sin(ωx+2φ)-sin(ωx+2φ)+sinωx
=sinωx,
由$\frac{π}{2}$+$2kπ≤ωx≤2kπ+\frac{3π}{2}$,(k∈Z)上单调递减,
得:$\frac{π}{2ω}$+$\frac{2kπ}{ω}≤x≤\frac{2kπ}{ω}+\frac{3π}{2ω}$,
∴函数f(x)的单调减区间为:[$\frac{2kπ}{ω}$$+\frac{π}{2ω}$,$\frac{2kπ}{ω}+\frac{3π}{2ω}$],(k∈Z).
∵在(π,$\frac{3π}{2}$)上单调递减,
可得:$\left\{\begin{array}{l}{\frac{2kπ}{ω}+\frac{π}{2ω}≤π}\\{\frac{2kπ}{ω}+\frac{3π}{2ω}≥\frac{3π}{2}}\end{array}\right.$⇒$\left\{\begin{array}{l}{2k+\frac{1}{2}≤ω}\\{\frac{4k}{3}+1≥ω}\end{array}\right.$,(k∈Z).
∵ω>0,
当k=0时,
可得:$\frac{1}{2}≤$ω≤1.
考查选项,故选C.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案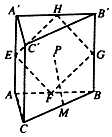 如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )| A. | 2 | B. | 2π | C. | $2\sqrt{3}$ | D. | 4 |
| A. | ?x∈(-∞,0),x3+x<0 | B. | ?x∈(-∞,0),x3+x≥0 | ||
| C. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}<0$ | D. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}≥0$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| 分数区间 | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] |
| 人数 | 2 | 8 | 32 | 38 | 20 |
(2)现从成绩在[70,110)中按照分数段,采取分成抽样的方法随机抽取5人,再在这5人中随机抽取2人作小题得分分析,求恰有1人的成绩在[70,90)上的概率.
| A. | $\frac{3}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
| A. | -2i | B. | 2i | C. | -i | D. | i |
| A. | [$\frac{1}{3}$,+∞) | B. | [2,+∞) | C. | ($\frac{1}{3}$,2) | D. | [$\frac{1}{3}$,2] |
 如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=$\frac{1}{2}$BC=2,AC=CD=3.
如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=$\frac{1}{2}$BC=2,AC=CD=3.