题目内容
4.已知命题p:?x0∈R,lnx0≥x0-1.命题q:?θ∈R,sinθ+cosθ<1,.则下列命题中为真命题的是( )| A. | p∧q | B. | (¬p)∧q | C. | (¬p)∧(¬q) | D. | p∧(¬q) |
分析 先判断命题p和命题q的真假,进而根据复合命题真假判断的真值表,得到答案.
解答 解:?x0=1∈R,使lnx0=x0-1=0.
故命题p:?x0∈R,lnx0≥x0-1为真命题,
当θ=$\frac{π}{4}$时,sinθ+cosθ=$\sqrt{2}$>1,
故命题q:?θ∈R,sinθ+cosθ<1为假命题,
故命题p∧(?q)为真命题,
命题(?p)∧q,(?p)∧(?q),p∧q为假命题,
故选:D.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,全称命题和特称命题等知识点,难度中档.

练习册系列答案
相关题目
19.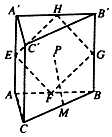 如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
 如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )| A. | 2 | B. | 2π | C. | $2\sqrt{3}$ | D. | 4 |
16.侧面都是直角三角形的正三棱锥,底面边长为a时,该三棱锥的全面积是( )
| A. | $\frac{3+\sqrt{3}}{4}$a2 | B. | $\frac{3}{4}$a2 | C. | $\frac{3+\sqrt{3}}{2}$a2 | D. | $\frac{6+\sqrt{3}}{4}$a2 |
14.在区间[1,5]随机地取一个数m,则方程m2x2+4y2=1表示焦点在y轴上的椭圆的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |