题目内容
13.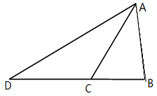 如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.
如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.
分析 利用余弦定理,求出∠ACB=60°,∠ACD=120°,在△ACD中,AC=10,∠ADB=30°,∠ACD=120°,利用正弦定理可得结论.
解答 解:在△ABC中,AB=10,AC=14,BC=6,
由余弦定理得$cos∠ACB=\frac{{A{C^2}+B{C^2}-A{B^2}}}{2AC•BC}=\frac{100+36-76}{2×10×6}=\frac{1}{2}$,
所以∠ACB=60°,∠ACD=120°,
在△ACD中,AC=10,∠ADB=30°,∠ACD=120°,…8分
由正弦定理得,$\frac{AC}{sin∠ADB}=\frac{AD}{sin∠ACB}$
所以$AD=\frac{AC•sin∠ACB}{sin∠ADB}=\frac{{10•sin{{120}°}}}{{sin{{30}°}}}=10\sqrt{3}$…12分.
点评 本题考查正弦、余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
18.f(x)=x(x-c)2在x=2处有极小值,则常数c的值为( )
| A. | 2 | B. | 6 | C. | 2或6 | D. | 1 |
3.甲、乙两人的各科成绩如茎叶图所示,则下列说法正确的是( )
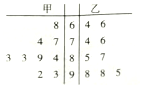

| A. | 甲的中位数是89,乙的中位数是98 | |
| B. | 甲的各科成绩比乙各科成绩稳定 | |
| C. | 甲的众数是89,乙的众数是98 | |
| D. | 甲、乙二人的各科成绩的平均分不相同 |
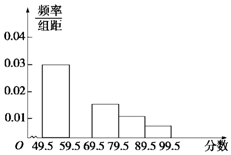 在长丰中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.
在长丰中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.