题目内容
2.椭圆与双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$的焦点相同,且椭圆上一点到两焦点的距离之和为10,则椭圆的离心率为$\frac{4}{5}$.分析 由双曲线方程求出椭圆的焦距,再由定义求得长轴长,代入离心率公式得答案.
解答 解:由双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$,得c2=4+12=16,∴c=4.
∴椭圆与双曲线的焦距相等为2c=8.
又椭圆上一点到两焦点的距离之和为10,即2a=10.
∴椭圆的离心率为e=$\frac{2c}{2a}=\frac{8}{10}=\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查椭圆与双曲线的简单性质,考查椭圆定义的应用,是基础的计算题.

练习册系列答案
相关题目
12.已知${({1+x})^{10}}={a_0}+{a_1}({1-x})+{a_2}{({1-x})^2}+L+{a_{10}}{({1-x})^{10}}$,则a8等于( )
| A. | -5 | B. | 5 | C. | 90 | D. | 180 |
10.下列图形中,不可能是函数y=f(x)的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
14.cos555°的值为( )
| A. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | C. | $-\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ |
11.执行如图所示的程序框图,则输出的S的值为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
9.“x>1”是“x>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
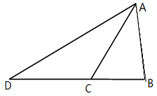 如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.
如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.