题目内容
18.f(x)=x(x-c)2在x=2处有极小值,则常数c的值为( )| A. | 2 | B. | 6 | C. | 2或6 | D. | 1 |
分析 根据函数在x=2处有极小值,得到f′(2)=0,解出关于c的方程,再验证是否为极小值即可.
解答 解:∵函数f(x)=x(x-c)2,
∴f′(x)=3x2-4cx+c2,
又f(x)=x(x-c)2在x=2处有极值,
∴f′(2)=12-8c+c2=0,
解得c=2或6,
又由函数在x=2处有极小值,故c=2,
c=6时,函数f(x)=x(x-c)2在x=2处有极大值,
故选:A.
点评 本题考查函数在某一点取得极值的条件,是中档题,本题解题的关键是函数在这一点取得极值,则函数在这一点点导函数等于0,注意这个条件的应用.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
8.已知方程$\frac{x^2}{2-k}+\frac{y^2}{2k+1}=1$表示焦点在y轴上的椭圆,则实数k的取值范围是( )
| A. | $(\frac{1}{2},2)$ | B. | (2,+∞) | C. | (1,2) | D. | $(\frac{1}{2},1)$ |
6.已知x,y满足$\left\{\begin{array}{l}y≤x\\ x+y+2≥0\\ x≤1\end{array}\right.$,且z=y-2x的最大值是( )
| A. | 1 | B. | -1 | C. | -2 | D. | -5 |
3.如图,A,B是以点C为圆心,R为半径的圆上的任意两个点,且|AB|=4,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=( )


| A. | 16 | B. | 8 | C. | 4 | D. | 与R有关的值 |
10.下列图形中,不可能是函数y=f(x)的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
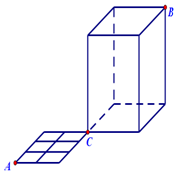 如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.
如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.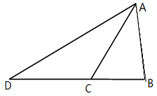 如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.
如图,在△ABC中,AC=10,$AB=2\sqrt{19}$,BC=6,D是边BC延长线上的一点,∠ADB=30°,求AD的长.